이전 글에서는 Dijkstra's Shortest-path Algorithm 방식에 대해서 정리해 보았다. 이번 글에서는 플로이드의 알고리즘을 통해 그라프의 최단 경로를 찾는 방법에 대해 정리해 볼 예정이다.
1. Adjacency matrix
플로이드의 알고리즘에 대해서 정리하기 전에, 플로이드 알고리즘의 기본 아이디어 예시를 한 번 살펴보려고 한다. 예시 그라프에 대해 다음 인접 행렬이 존재한다고 가정해보자.


위의 인접 행렬 A는 각 vertex에 경로가 존재하면 1, 아니면 0으로 표시한 Boolean matrix이다. 따라서 이 행렬의 곱셈은 logical 연산을 통해 수행 되는데, 이를 이용해 A^2과 A^3을 구하면 다음과 같다.


이때, A^2의 행렬을 통해 그라프를 다시 그려보자. 그럼 다음과 같은 그라프가 나온다.

이때, 기존 그라프에서 2개의 edge를 거쳐 도달할 수 있는 경우를 생각해보고, adjacency 행렬로 만들고 그 행렬을 A'이라고 한다면, 이는 정확히 A^2과 일치한다. 즉, A^2의 의미는, 한 노드에서 2개의 edge를 거쳐 도달할 수 있는 vertex에 대해 존재하면 1, 아니면 0으로 표시한 Boolean matrix이다.
그렇다면 A^3의 경우는 어떨까? A^3의 경우도 기존의 그라프에서 3개의 edge를 거쳐서 갈 수 있는 vertex가 존재하면 1, 아니면 0으로 표시한 것과 같다.
이제 다음 식을 확인해보자.

여기서 I~A^3 사이에 사용된 연산은 OR 연산을 의미한다. 즉, 이식은 한 정점에서 다른 정점까지 경로가 존재하는지 확인하기 위한 reachability matrix이다. 이는 실제 플로이드 알고리즘에서 경로 존재 여부를 계산할 때 이용이 된다.
여기서 생기는 의문점은 A^∞인데, 왜 A^3까지만 OR 연산으로 합치는 것이냐이다. 즉, A^4, A^5 같은 항이 빠져서 부족하지 않느냐는 의문이 생길 수 있다. 그런데 이렇게 표현하는 이유는 다음과 같다.
가 의미하는 바는 정확히 4개의 edge를 거쳐 도달할 수 있는 vertex의 존재 여부이다. 이는 곧 그래프 내에서 사이클을 포함한 경로까지 고려하는 것이고, 앞서 등장한 , A^2, A^3에서 이미 한 번 이상 포함된 경로들과 중복된 정보가 된다.
따라서, 조금 더 일반적으로 정리하자면 n개의 정점이 존재하는 그라프 G에 대해서 A^
즉, 그라프 G에 대해 Boolean adjacency matrix를 A라고 하고, A^를 위와 같은 식으로 표현하면, A^∞는 그래프에 존재하는 모든 경로의 존재 여부를 나타내는 행렬이 된다.
2. All-pairs Shortest Path
이제, 본격적으로 위의 인접 행렬을 이용해 그라프의 최단 경로들을 찾아보자. 이 방법에 대해 알아보기 전에, 먼저 다음과 같은 명제들을 알고 넘어가자.
- 1,~n까지의 vertices가 있다고 가정하자. 이때, 1<=l<=n을 만족하는 l에 대해서, 다음이 성립한다.
- 만약, v1~vl이 v1~v1까지의 최단경로라면, 1<=m<=l을 만족하는 m에 대해서, v1,..,vm, vm,..,vl 둘 다 가장 짧은 path이다. 또한, 1<=k<=l을 만족하는 k에 대해서도 똑같이 적용된다.
위 명제를 증명하기위해, v1~vl이 최단경로이지만, v1~vm이 가장 짧은 경로가 아니라고 해보자. 그리고, v1'~vm'까지를 이보다 더 짧은 경로라고 하자. 그러면, v1~vl은 v1~vm~vl보다 짧은 경로인 v1~v(m-1)'vm~vl이 된다. 이 순간 모순이 생기므로, v1~vm은 최단 경로임을 증명할 수 있다.
위 명제를 통해, 우리는 최단 경로도, Dynamic Programming을 통해 해결할 수 있을 것 같다는 생각을 가질 수 있다.
- 다음 방정식이 성립한다.
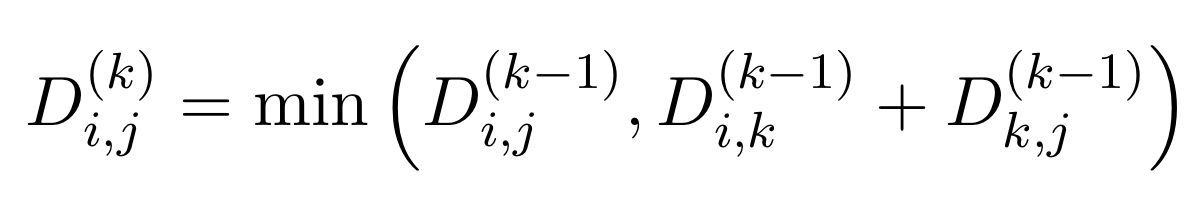
식에 대해서 설명하면,
- i~j의 최단경로를 구할 때, 중간 정점은 1~k까지 정점만을 사용하고, min통해 최단 경로를 구한다.
- 중간 정점이 k보다 작을 경우, i~j까지의 최단 경로는 중간정점이 1~(k-1)에 존재한다는 것이다.
- 중간 정점이 k일 경우, i~k까지의 최단경로와 k~j까지의 최단경로의 합이 i~j까지의 최단 경로이다.
- 따라서 둘 중 최솟값이 결국 i~j까지의 중간정점 (1~k)를 포함한 최단 경로가 된다.
이 방정식을 유념해 두며 다음 그림의 그라프를 살펴보자.
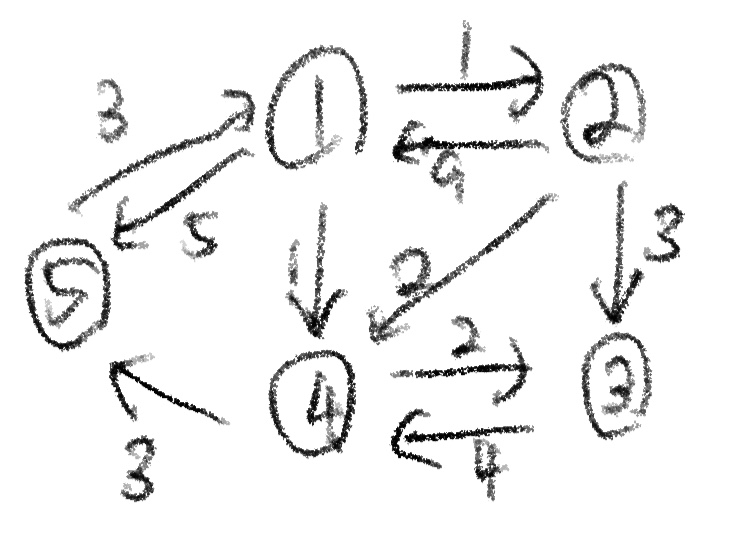
위 그라프에 대해서 A와 동일한 개념의 행렬 D를 구하면, 다음과 같다.
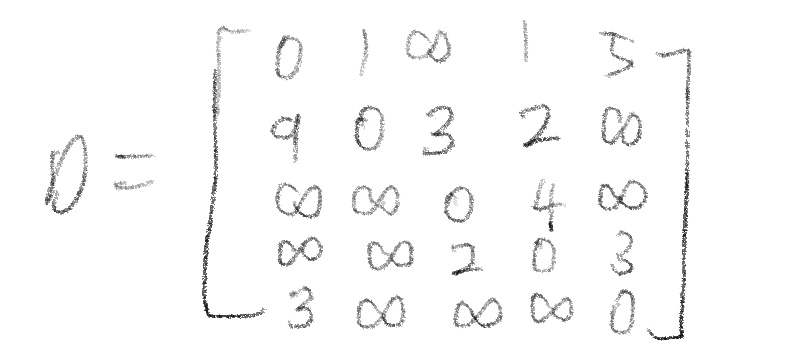
우리는 위에서, D^(n-1)까지의 OR 연산으로 D^∞를 나타낼 수 있다고 정리했지만, 즉 여기서는 4까지만으로도 충분하지만, 일반화를 위해, 다음 처럼 D를 D^n까지로만 나타낸다고 가정하자.
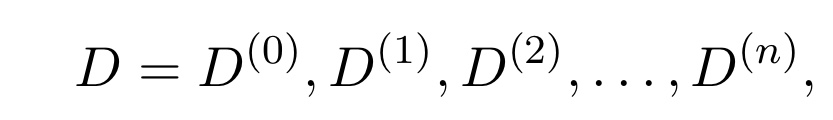
그럼, 이제 이 그라프에 대한 최단경로를 구하는 코드를 한 번 살펴보자.
P : n by n global array for reconstructing the shortest paths
floyd(D) //input : distance matrix
{
Init:
D(0) <- D; P = all zero.
Main Loop:
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1; j<=n; j++)
if( D(k-1)(i,k) + D(k-1)(k,j) < D(k-1)(i,j) )
D(k)(i,j) <- D(k-1)(i,k) + D(k-1)(k,j)
P(i,j) <- k
else
D(k)(i,j) <- D(k-1)(i,j)
}
path(i,j)
{
if P(i,j) != 0
path(i, P(i,j))
print(P(i,j)
path(P(i,j) , j)
}
위의 코드를 적용하면, 출력결과는 다음과 같이 나온다.

즉, 예를들어, P(2,1)=5라는 뜻은, 2~1로가는 최단경로는 중간 노드 5를 꼭 거친다는 것이다. 즉 경로는 2..5..1로 설정되고 다시 2..5에 최솟값이 있는지, 5..1에 최솟값이 있는지 찾는다. 이처럼, 최단 경로를 구성할 때, 각 중간 정점을 저장하고 재귀적으로 따라가는 구조는 Dynamic Programming으로 풀 수 있다.
그럼 이 All-pairs shortest path의 시간 복잡도는 어떻게 될까? 명백하게 O(n^3)이 된다. 그 이유는 코드를 보면 확인 할 수 있다.
- 중간 정점 k의 범위: 1~n
- 출발 정점 i의 범위: 1~n
- 도착 정점 j의 범위: 1~n
총 세 겹의 반복문이 중첩되어 있어, 각 조합마다 수행되는 연산 수는 n*n*n=n^3이다. 또, 각 반복마다
- 최솟값 비교 연산 1회
- D[i][k]+D[k][j] 덧셈 연산 1회
- 조건 참일 경우, D[i][j] 최솟값, P[i][j]=k 대입 연산 2회
가 일어나고, 위 세 연산은 O(1) 내에 수행되기 때문에 전체 시간 복잡도는 O(n^3*1) = O(n^3)이다.
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Alogrithm_Dijkstra's Shortest Path Algorithm (0) | 2025.06.07 |
|---|---|
| [알고리즘 분석] - Graph Algorithm_Strongly Connected Components (0) | 2025.06.06 |
| [알고리즘 분석] - Graph Algorithm_BFS, DFS (1) | 2025.06.06 |
| [알고리즘 분석] - huffman code (0) | 2025.05.23 |
| [알고리즘 분석] - 분할 정복(divide and conquer) (1) | 2025.04.20 |



