지난 글에서는 Dynamic programming이라는 알고리즘 방식을 쓰는 여러 문제들을 정리했다. 이번에는 huffman code에 대해서 정리해보려고 한다.
1. huffman code란?
기본적으로, 컴퓨터는 문자를 그대로 인식하지 못하고, 이진수로 변경해줘야 한다. 예를 들어, 다음과 같이 알파벳에 대한 이진수가 정의돼 있다고 가정해보자.

그리고 다음과 같은 문자열이 주어졌다고 가정해보자.
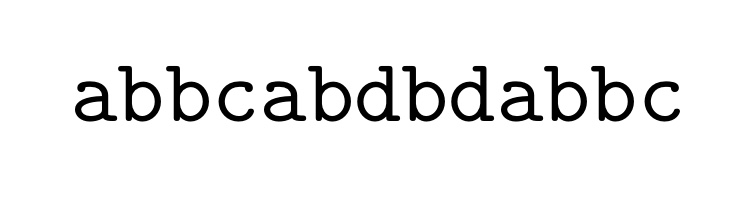
이를 주어진 문자열에 대한 이진수로 바꾸면 다음과 같다.

이렇게, 문자열을 이진수로 바꾸는 과정을 encoding이라고 하고,
반대로 이진수를 주어진 알파벳에 대응하여 문자열을 만드는 과정을 decoding이라고 한다.
위의 예시는 13자리 문자열에 대해 26bit로 encoding이 됐다.
1.2 Prefix-free code
위의 예시는 문자 하나당 bit수가 2bit로 정해져 있었다. 그렇지만, 굳이 비트 수를 고정시켜서 할당할 필요 없이 다음과 같이 진행해도 된다.

위와 같이 똑같은 13자리 문자열을 encoding 하게 된다면, 다음과 같은 결과가 나온다.

위는 총 25bit로 첫 번째 경우보다 bit수가 1자리 줄었다.
또 재밌는 점은, 위의 a,b,c,d,에 대한 이진수는 다음과 같은 binary tree로 만들 수 있다는 것이다.
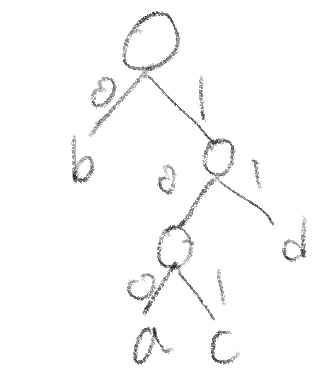
위의 25 bit를 계산할 때, endcoding 후 bit를 하나하나 다 세서 구할 수 도 있지만, a가 3개 등장했고, b가 6개 등장했고, c가 3개 등장했고, d가 2개 등장했으니 각각의 bit 수에 등장한 갯수를 곱해서 구할 수도 있다.
그럼 반대로, decoding을 할 때는 어떨까? 위의 binary tree를 참고하면, decoding은 쉽게 가능하다. 이렇듯, 이렇게 구현된 code는 prefix-free code라고 한다. 그렇지만, binary tree로 나타낼 수 없는 경우, 예를 들어 c=10으로 바뀐다면, 두 가지 이상의 decoding 경우의 수가 발생하기 때문에, decoding이 불가능해진다. 컴퓨터는 이를 고려하여 설계돼야 한다.
1.3 huffman code
허프만 코드는 임의의 문자열에 대해서 인코딩을 진행할 때, 제일 bit수가 짧게 나오게 만드는 인코딩 방식이다. 위의 문자열에 대해서 대응하는 비트만 다음과 같이 바꿨다고 가정해보자
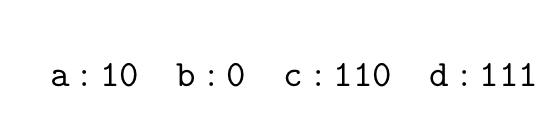
이렇게 바꾸게 되면, binary tree는 다음과 같이 나온다.
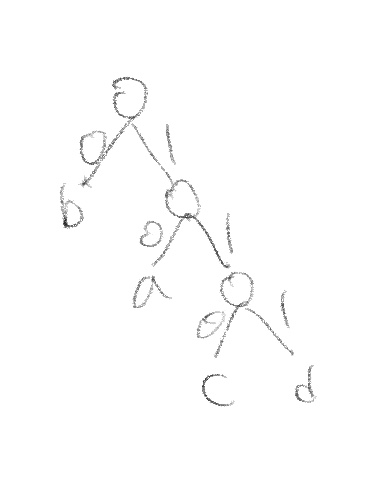
그리고, 이 때, encoding된 bit수를 계산하면, 총 24bits가 나오게 된다. 직전 예시보다 1비트가 더 줄었다.
bit수를 구하는 곱셈과정을 한 번 다시 생각해보자. 기본적으로, 문자열에서 제일 많이 등장하는 문자, 위의 예시를 들면 b(6번)에 대해서 해당하는 비트 수가 적고, 그 다음으로 많이 등장하는 문자 a나 c(3번)에 대해서 그 다음으로 비트 수가 적게 할당하면, bit 수가 최소가 되게 encoding을 할 수 있겠다는 생각이 들 것이다. 이 방식이 바로 huffman-code 알고리즘이다.
1.4 huffman code의 구현 방식
기본적인 아이디어는 바로 윗 문단에서 설명했다. 이를 구현하기 위한 아이디어는 다음과 같다.
- 먼저, 해당 문자가 문자열에 몇 번 등장했는지 계산한다.
- 그 뒤, 가장 적게 나온 두 친구를 더한다
- 결과값이 나오고, 그 결과값과 나머지 등장 횟수 중에서 가장 적게 나온 두 친구를 더한다.
- 위 과정을 반복한다.
처음 예시대로 위 과정을 적용시켜 진행하면, 다음과 같다.
- a:3, b:6, c:3, d:1
- 가장 적게 나온 d와 a/c를 더한다(빈도수가 같다면 아무거나 더해줘도 된다)
- c를 더했다고 가정해보면, 3,6,5 중 가장 작은 수 2개를 더한다
- 8,6이 남게 되고 최종적으로 14이 나온다.
이를 토대로 binary tree를 그릴 수 있는데, 다음과 같이 나온다.

즉, 문자열 예시에 대해 가장 적게 나왔던 트리 구조와 똑같이 나오게 된다. 이를 좀 더 일반화 시켜보자.
다음 상황을 가정하자.
- 문자열을 구성하는 문자 n개가 a1,a2,a3,...,an으로 존재한다.
- 각각의 빈도수를 f1,f2,f3,...,fn이다.
그리고 다음과 같은 형태로 binary tree가 존재한다고 가정해보자.

위 트리는 internal node의 수가 8개, leaf node의 수가 9개인 binary tree이다.
이 때, 이를 빈도수에 대한 트리, 즉 fn에 대한 트리로 만들면 다음과 같이 나타낼 수 있다.

이 때, di를 fi에 대한 트리의 깊이라고 했을 때, encode할 문자열의 총 비트수는 다음과 같이 나타낼 수 있다.
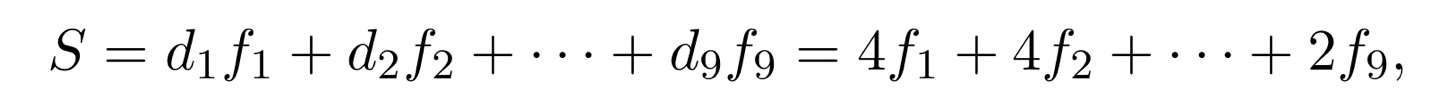
위의 식과 binary tree를 비교해 보면, S는 다시 internal node들의 합으로 나타낼 수 있다. f1의 d1, 즉 깊이는 4이다. 이 때, f1의 루트 노드로 가는 경로 상에 f1은 4번 나타나게 된다. 즉, internal node에 나타난 수와 깊이가 같다는 것이다. 이를 식으로 나타내면 다음과 같다.

그래서, 주어진 문자열의 총 비트 수를 구하려면, internal node의 합만 구해줘도 된다. 이를 "path length lemma"라 부리기도 한다.
이제, huffman code의 트리를 Tn이라 하고, 다음 상황을 가정하자.
- Tn의 leaf node에 들어갈 키값들을 w1,w2,w3,...,wn이라고 하자.
- 이 키값들 중 제일 작은 키값 두개를 w1,w2라고 하자.
이때, 다음이 성립함을 알 수 있다.
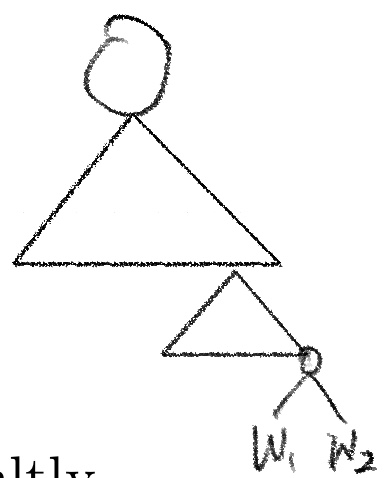
- Tn은 Tn-1이라는 subtree와 (w1+w2)의 subtree로 나타낼 수 있다.
- 따라서 cost of Tn= cost of Tn-1 + (w1+w2)로 나타낼 수 있다.
이를 그림으로 나타내면 다음과 같다.
이때, 다음을 정의하자.
- Cost = frequency tree에서 inner-node의 총 합
- Tn = huffman code for {w1, w2, ..., wn}
- Tn-1 = huffman code for {w1+w2, w3, w4, ... , wn}
- T : optimal code for {w1, w2, ..., wn}
- T' : T에서 w1,w2를 w1+w2라는 subtree로 묶은 code tree {w1+w2, w3, ... , wn}
이때, cost of Tn = cost of Tn-1 + w1 + w2이다.
huffman code의 시간 복잡도는 어떻게 될까? 주어지는 값에 따라 달리지게 된다. 총 3가지가 있는데 한 번 살펴보자.
- O(n^2 logn) : (제일 작은 수 두 개 더하고 n-1개의 수를 다시 정렬)*(n번 반복) = O(n^2 logn)
- O(n^2) : 가장 작은 두 개의 frequencies을 select하는 과정 n번 반복 = O(n^2)
- O(nlogn) : priority queue를 이용한 방법
- frequency가 낮은 것이 제일 높은 priority를 가지게 pritority queue에 push한다. O(logn)시간이 걸린다.
- 제일 frequency가 낮은 2개의 두 수를 pop을 한 뒤 합친다. pop을 하고 다시 push하는 데 걸리는 시간은 2*O(logn)이다.
- 이 과정을 n-1번 반복하기 때문에 총 O(nlogn) 시간이 걸린다.
따라서 O(nlogn) 시간이 걸리는 priority queue를 이용하는 방법을 택하는 것이 좋다는 것을 알 수 있다.
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Algorithm_Strongly Connected Components (0) | 2025.06.06 |
|---|---|
| [알고리즘 분석] - Graph Algorithm_BFS, DFS (1) | 2025.06.06 |
| [알고리즘 분석] - 분할 정복(divide and conquer) (1) | 2025.04.20 |
| [알고리즘 분석] - 피보나치 (2) | 2025.04.17 |
| [알고리즘 분석] - 수도코드 및 시간 복잡도 (0) | 2025.04.16 |



