지난 글에서는 huffman code에 대해서 정리해 보았다. 이번 글부터는 graph algorithm에 대해서 정리해보려고 하는데, 이번 글에서는 BFS와 DFS의 개념 정리에다가 topological sorting까지만 정리해보려고 한다.
1. Graph란?
한 그라프의 이름을 G라고 하면, 이 G라는 그라프는 (V,E)의 쌍으로 이루어져 있다. 이 때, V는 vertices(꼭짓점), E는 edges(모서리, 엣지)이다. vertices는 tree로 치면 노드 같은 친구들이라고 생각하면 된다. 실제 값이 존재하고, edges들이 이 vertices 사이의 관계를 나타내 준다.
그라프의 종류는 다양하다. 나중에 다시 천천히 정리할 예정이지만, undirected graphs, directed graphs, 가중치가 있는 graphs 등 여러가지가 있다. 이 중 앞서 다뤘던 tree들도 cycle이 없는 그라프의 한 종류로 여겨질 수 있다.
앞으로 다음과 같이 n과 m을 각각 vertices와 edges의 수로 표시할 것이다.

undirected graph에서, 즉 edge들의 방향이 없는 상태에서, m은 O(n^2)임을 알 수 있다. 그 이유는 다음과 같다.
- n개의 꼭짓점은 본인 제외 n-1개의 꼭짓점과 모서리를 연결할 수 있다.
- m=n-1개가 되고, 이 경우가 n개의 꼭짓점에 대해 모두 독립적으로 존재하기 때문에 n*(n-1)이다.
- 이 때, 모서리의 방향성이 존재하지 않기 때문에 2로 나눠주게 되면, m=n*(n-1)/2가 된다.
이를 통해 우리는 m이 O(n)에 가까워질 수록 graph는 sparse하다고 표현하고, O(n^2)에 가까워질 수록 graph는 dense하다고 표현할 수 있다.
+)앞으로 다룰 그라프는 웬만하면 sparse한 그라프라고 생각하자.
또, 그라프는 컴퓨터에서 그림으로 나타낼 수 없기 때문에, adjacency matrix나 adjacency list로 구현하는다. adjacency matrix에서는 Θ(n^2) 공간 복잡도를, adjacency list에서는 Θ(n+m)의 공간 복잡도를 가지는 것을 알 수 있다.
2. Graph Traversal
Traversal은 tree에서도 쓰인 기법이다. 트리에서는 모든 노드를 방문하거나 특정 노드를 찾는 방법으로 쓰였다.
graph에서는 특정 vertex를 찾기보다는 모든 vertices를 방문하는 방법으로 traversal을 진행할 예정이다. 이 traversal을 진행하는 방식에 따라 2가지의 graph 유형이 나온다.
- BFS: Breadth-First Search
- DFS: Depth-First Search
BFS와 DFS를 차례대로 설명해보려고 한다.
3. BFS
먼저, BFS에 대해서 알아보자. 다음 그림의 graph에 대해서 BFS를 진행하려고 한다.

BFS의 Traversal 방법은 인접 vertices를 죄다 확인하는 방법이다. 다음과 같은 방법으로 진행된다.
- A에서 traversal을 시작한다고 가정.
- A의 인접 vertex인 B와 F를 확인.
- B로 이동한 뒤, B기준 A는 이미 확인된 vertex이므로, 그 다음 인접 vertex인 C, D, E 확인
- F로 이동한 뒤, F기준 A는 이미 확인된 vertex이므로, 그 다음 인접 vertex인 J 확인
- C,D,E,J에 대해 동일하게 진행
위 방법으로 진행한다면 다음과 같은 BFS tree가 나올 수 있다.
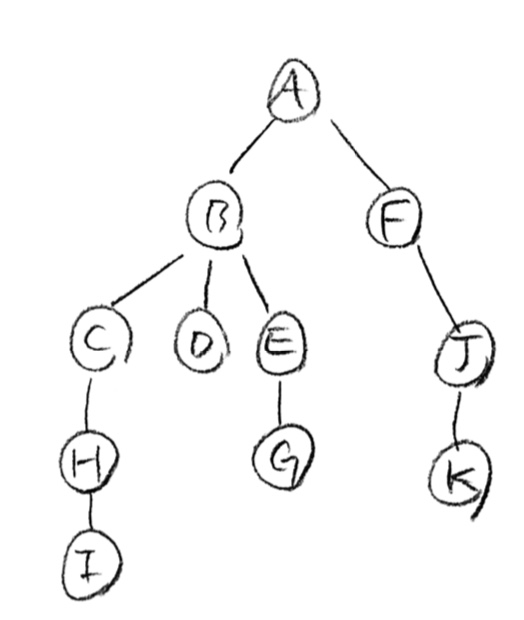
여기서 생기는 의문점 한 가지는, 왜 E에서 G까지만 하고 K와 J는 F쪽에서 탐색될까? 이 질문에 대한 답은 BFS traversal 방법이 queue를 이용하기 때문이다.
즉, 다시 설명하자면,
- A에서 시작하면, A의 인접 vertices인 B와 F가 순서대로 queue에 들어가고,
- queue에서 B가 빠져나올 때, B의 인접 vertices인 C,D,E를 queue에 넣는다.
- 그 다음에, queue에서 F가 빠져나올 차례니 F의 인접 vertex인 J가 queue에 들어가게 되고
- 같은 원리로 진행하다보면 위와 같은 트리가 나오게 된다.
이제, BFS에 대해서 더 자세히 알아보자.
BFS를 수도코드로 나타내려고 하는데, 다음과 같은 vertex의 상태가 필요하다.
- UNDISCOVERED : 아직 발견되지 않은 vertex
- DISCOVERED: 발견되었지만, neighbor들이 모두 확인되지 않은 상태
- PROCESSED: neighbor들까지 모두 확인된 상태
위와 같은 vertex의 상태를 가지고 BFS의 수도코드를 만들면 다음과 같다.
BFS(start)
{
initialize state[] # all UNDISCOVERED
state[start] <- DISCOVERED
push(start)
while(queue is not empty){
current <- pop()
for each neighbor v of current
if(state[v] = UNDISCOVERED) {
state[v] <- DISCOVERED
push(v)
}
state[current] <- PROCESSED
}
}
코드에 대해 설명하면,
- 처음에 모든 vertices를 UNDISCOVERED로 초기화한다.
- queue에 start vertex를 넣고, while문으로 이동한다.
- current를 start vertex를 queue에서 pop한 뒤 대응시킨다.
- current의 neighbor v에 대해 UNDISCOVERED된 상태라면 DISCOVERED로 상태를 변경하고 queue에 push한다.
- neighbor가 다 발견됐으면 current를 PROCESSED 상태로 변경한다.
- BFS가 끝나면, 그라프 내 모든 vertices은 PROCESSED 상태가 된다.
위 코드를 확인해 보면, 다음과 그림과 같은 경우가 나올 수 있다.

그림을 간단히 설명해보면, C와 D까지는 인접 vertices를 다 확인했기 때문에 PROCESSED된 상태이고, 이제 E가 PROCESSED될 차례이다. 이 때, H를 보면, DISCOVERED지만, 인접 vertex인 I가 아직 DISCOVERED된 상태가 아니기 때문에 PROCESSED 상태로 바뀔 수 없다.
위 그림을 참고하면, start에서 current vertex까지의 거리를 d라고 하면, 모든 PROCESSED된 vertices는 start로부터 거리가 d보다 작거나 같고, DISCOVERED된 vertices는 d+1보다 작거나 같음을 알 수 있다.
이제, 실제로 BFS-tree를 만들 때 코드로는 어떻게 구현해야 되는지 알아보자. 다음 코드를 살펴보자.
{
initialize state[] and parent[] //parent[start] <- -1
...
while (queue is not empty) {
current <- pop()
for each neighbor v of current
if (state[v] = UNDISCOVERED) {
state[v] <- DISCOVERED
push(v)
parent[v] <- current
}
state[current] <- PROCESSED
}
}
앞선 기본 BFS와 비슷한 코드로 진행되지만, parent[]라는 배열이 생겼다.
parent[] 배열이 하는 역할을 살펴보자. 만약, 어떤 current에 대해 vertex v가 UNDISCOVERED 상태라면, DISCOVERED 상태로 바꾸고, current는 vertex v의 parent가 되며, parent[v] 값에 current를 넣는다. 이렇게 v-current 사이에 부모-자식 관계가 생기게 된다.
그럼, 굳이 parent[]라는 배열을 추가한 이유는 뭘까?
우리는 BFS-tree를 통해 임의의 2개의 점의 가장 짧은 거리를 찾고 싶다. 이때 parent[] 배열을 사용하면, 각 정점이 어느 정점으로부터 탐색되었는지를 기록할 수 있어, 목적지에서 시작점까지 경로를 역추적할 수 있게 된다. 이렇게 하면 BFS 탐색을 통해 발견된 최단 경로를 실제로 복원하고 출력할 수 있다. 다음 코드를 한 번 살펴보자
shortest_path(s,t)
{
state[s] <- DISCOVERED
push(s)
parent[s] <- -1
while(queue is not empty) {
current <- pop()
for each neighbor v of current
if(state[v] = UNDISCOVERED) {
state[v] <- DISCOVERED
push(v)
parent[v] <- current
if(t=v) //found t!
return 1
}
state[current] <- PROCESSED
}
return 0 // the traversal is complete without finding t
}
위 코드는 기존 BFS 코드에서 if (t == v) 조건절을 추가하여, s에서 t까지의 최단 경로를 찾으면 탐색을 종료하는 방식이다. if (t == v)가 if (state[v] == UNDISCOVERED) 조건문 안에서 작동하는 이유는, 한 정점이 처음으로 큐에 들어가는 순간, 즉 UNDISCOVERED 상태에서 DISCOVERED 상태가 되는 그 순간이 바로 최단 경로가 결정되는 시점이기 때문이다. 따라서 이때의 v가 우리가 찾는 목적지 t라면, 그 경로가 최단 경로이므로 탐색을 즉시 종료해도 되는 것이다.
그렇다면 이제, 실제로 parent[] 값을 활용하여 최단 경로를 출력하는 코드를 살펴보자 .
print_path(s,t)
{
p[]; //long enough to save the path
v<-t; i<-0
while (v!=s) {
p[i++] <-v
v<-parent[v]
}
p[i] <-s
while(i>=0)
print p[i--]
}
위 코드는 s에서 t까지의 최단 경로를 print하는 함수이다. 위 코드에 대해서 설명해보면,
- p[]는 s에서 t까지의 경로를 저장할 배열이다.
- v를 t로 초기화하고, 인덱스 i는 0으로 설정한다.
- v가 s가 될 때까지 반복하며, v를 배열에 넣고 v를 parent[v]로 갱신한다.
- 마지막으로 시작점 s를 배열에 추가한다.
- 이 배열은 s에서 t까지의 경로가 역순으로 저장되어 있으므로, 출력 시에는 역순으로 출력해야 한다.
따라서, BFS 탐색 중 각 정점의 부모를 기록하는 parent[] 배열을 이용하면, 두 정점 간의 실제 최단 경로를 재구성할 수 있다. 이것이 parent[] 배열을 추가한 이유이다.
4. DFS

이제 위의 그라프를 DFS(Depth-First Search) 방법으로 나타내보자. DFS는 일단 무작정 보이는 vertex로 이동하는 것이다. 다음과 같은 순서로 진행된다.
- A에서 탐색을 시작한다고 가정.
- BFS 방법과는 달리 B,F를 모두 확인하는 것이 아니라 무조건 한쪽 vertex로 이동한다. 이때, 먼저 B로 이동한다고 가정.
- B에서도 무조건 한 vertex로 이동하기 때문에, 이번에는 C로 이동한다고 가정
- H-I까지 탐색을 완료한 뒤, 더 이상 새로 발견할 vertex가 없기 때문에 다시 재귀적으로 돌아간다.
- B에서 다시 또 새롭게 발견할 vertex D/E가 존재. 이때 D로 이동한다고 가정
- D에서는 F까지 계속 탐색.
- F에서 A는 이미 탐색완료한 vertex이기 때문에 다시 B까지 역순으로 돌아가며 더 새로운 vertex 없는지 확인
- 없고, B에서 A로 돌아간 뒤, 새롭게 발견할 vertex 없기 때문에 탐색 종료
위의 순서대로 탐색을 진행하면 다음 그림과 같이 DFS tree가 나오게 된다.
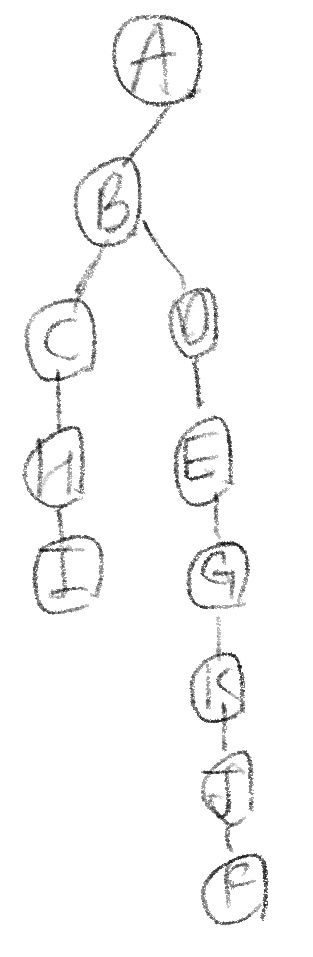
그럼 이 DFS도 한 번 수도코드로 알아보자.
DFS(s)
{
state[s] <- DISCOVERED
for each neighbor v of s
if(state[v] = UNDISCOVERED)
parent[v] <- s
DFS(v)
state[s]<-PROCESSED
}
위의 수도코드에 대해서 설명하면,
- s라는 vertex를 DISCOVERED 상태로 바꾸고,
- s의 이웃 정점 v 중에서 UNDISCOVERED 상태인 정점에 대해
- v의 부모를 s로 설정한다 (이후 경로 복원에 사용)
- DFS(v)를 재귀적으로 호출한다.
- 더 이상 새롭게 탐색할 정점이 없다면, s를 PROCESSED 상태로 바꾼다.
예를 들어 I까지 도달했을 때, I의 이웃 정점은 모두 방문 완료 상태이므로 I를 PROCESSED 상태로 바꾼다. 그리고 재귀적으로 호출한 순서에 따라 C → H → B로 되돌아오며, 이들 또한 더 이상 탐색할 이웃이 없기 때문에 각각 PROCESSED 상태가 된다. 하지만 B로 돌아왔을 때 아직 D라는 UNDISCOVERED 정점이 남아 있다면, 그쪽으로 다시 탐색을 이어가며 DFS는 계속된다.
+) BFS에서는 queue 방식을 썼지만, DFS에서는 stack 방식을 쓴다. 만약, A에서 시작했다면 A를 먼저 stack에 집어넣고 마지막에 꺼내며 PROCESSED 상태로 바꾸는 방식을 쓴다.
DFS의 stack(FILO) 방식 때문에 timestamp를 출력하는 코드를 다음과 같이 짤 수 있다.
t<-0 //global variable for timestamp
DFS(s)
{
state[s] <- DISCOVERED
t<-t+1;
discovery[s] <- t //discover time
for each neighbor v of s
if(state[v] = UNDISCOVERED)
parent[v] <- s
DFS(v)
state[s] <- PROCESSED
t<-t+1;
finish[s]<-t //finish time
}
위 코드에 대해서 설명하면, 한 vertex가 DISCOVERED된 time(=stack에 처음 들어간 time)과 한 vertex가 PROCESSED된 time(=stack에서 나온 time)을 DFS를 진행할 때 동시에 기록하는 코드이다.
위 코드를 통해, DFS tree에 timestamp까지 추가해서 나타내면 다음 그림과 같다.
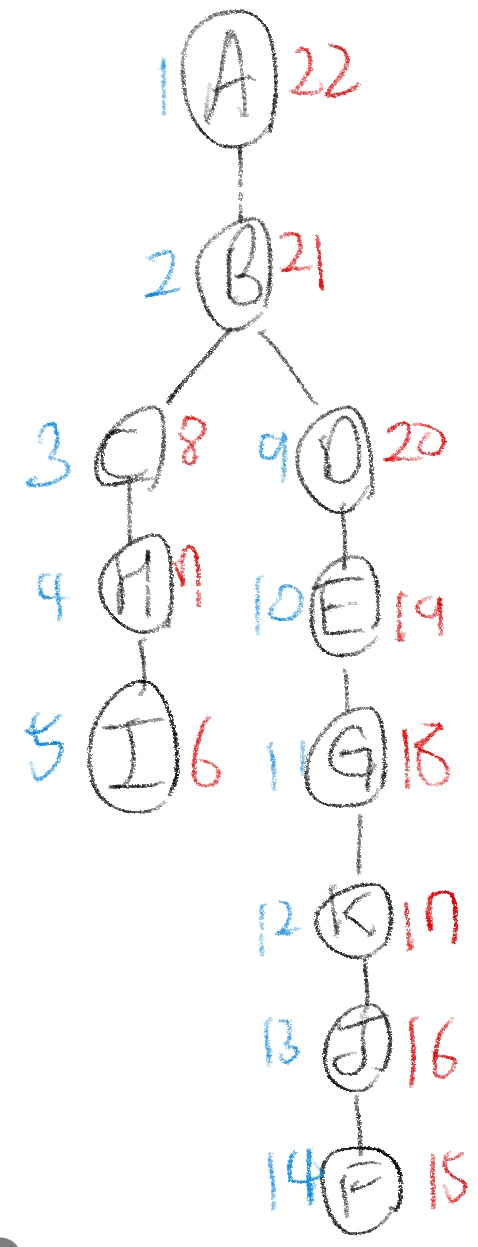
각 vertex의 왼쪽에 파란색으로 표시한 부분이 discovery time, 오른쪽에 빨간색으로 표시한 부분이 finish time으로 기록한 것이다. 위 그림을 참고하면, DFS가 stack 방식으로 작동하는 것을 더 쉽게 이해할 수 있다.
위와 같은 timestamp를 다음 그림과 같이 '('(=discovery time), ')'(=finish time)으로 나타낼 수 있다.

위 그림에 1-22는 A의 timestamp, 2-21은 B의 timestamp 처럼 각 괄호를 짝지어 vertex에 대한 timestamp를 나타낼 수 있다.
이제, vertex u,v에 대해 discovery time, finish time을 각각 [d(u),f(u)], [d(v),f(v)]로 표현하면, 다음을 정의할 수 있다.
- [d(u),f(u)]와 [d(v),f(v)]가 둘 다 서로의 descendant가 아니라면, disjoint하다.
- [d(u),f(u)]가 [d(v),f(v)]에 속해 있다면, u는 v의 descendant이다.
- [d(u),f(u)]가 [d(v),f(v)]를 포함한다면, u는 v의 d ascendant이다.
위의 DFS tree의 timestamp를 예를 들면, [d(C),f(C)]가 [d(I),f(I)]를 포함하고 있기 때문에, C는 I의 descendant이다.
또, [d(C),f(C)]와 [d(E),f(E)]는 timestamp가 겹치지 않기 때문에, 즉 교집합이 없기 때문에 둘은 disjoint한 상태이다.
이때, 위의 DFS tree와 원래 graph를 한 번 차례대로 살펴보자. Graph에서는 vertex A와 F, B와 E 사이에 edge가 존재하지만, DFS tree에서는 이 edge들이 나타나지 않았다. 이러한 edge들을 우리는 Back Edge라고 정의한다.
이를 일반화시켜 정리하면, 그라프 G = (V,E)에 대해서
- Edge(u,v)가 E에 속해있고, u의 이웃으로써 v가 처음 발견된 상태면 이를 tree edge라고 한다.
- Edge(u,v)가 E에 속해있고, v가 u의 ancestor라면, 즉, v가 먼저 발견된 상태라면 이를 back edge라고 한다.
그라프에서는 위의 두 종류의 edge말고 더 존재하는데, 후에 forward edge와 cross edge에 대해서도 다룰 예정이다.
그리고 DFS는 다음과 같은 정의들도 존재한다.
- 만약, DFS를 실행하는 graph가 undirected graph라면, 모든 edge는 tree edge나 back edge로 표현된다.
- 그라프 G에 cycle이 존재하면, G에 대한 DFS tree는 back edge가 존재한다.
4. Topological Sorting of DAG(Directed Acyclic Graph)
앞서, BFS와 DFS에 대해서 정리할 때, 모두 undirected graph에 대해서만 정리했다. BFS와 DFS는 undirected graph에만 적용되는 것이 아니라 directed graph에도 적용될 수 있다. 이번에는 DFS를 이용한 topological sorting을 정리할 예정이다.
먼저 다음 그림을 살펴보자.
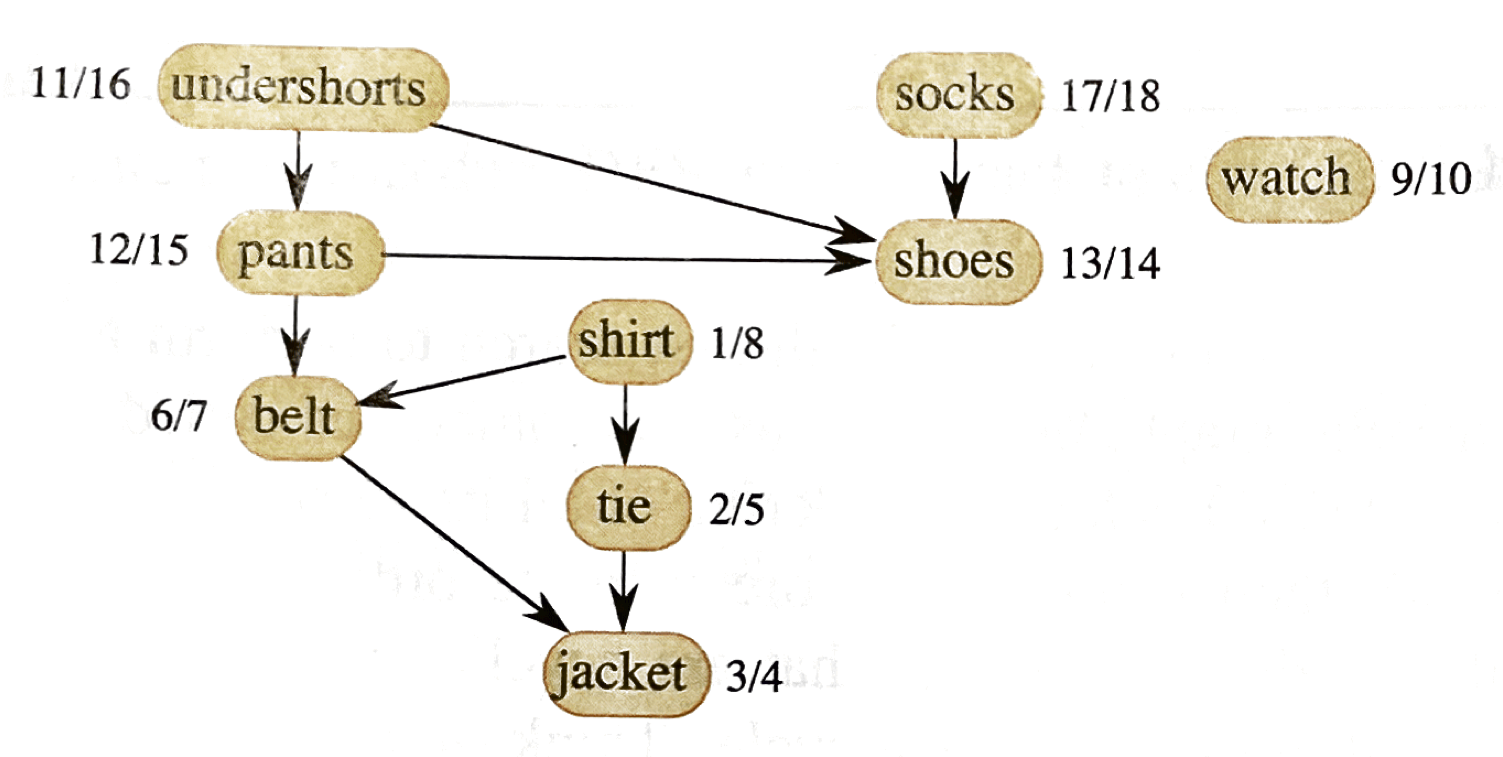
위 그림은, 확실히 방향성이 존재하는(directed) edge들로 구성된 그라프이며, DFS를 진행한 상태이다. 각각의 vertex에 대해서 discovery time과 finish time이 기록되어 있다. Topological sorting은 다음과 같은 순서로 진행된다.
- Directed Graph에 대해 DFS를 진행하고 timestamp를 기록한다.
- Finish time이 큰 순으로 왼쪽부터 차례대로 배치한다.
- 그리고, 모든 directed edge들을 표시한다.
위 순서대로 topological sorting을 진행하면 다음과 같은 그림이 나온다.

해당 그림에 대한 topological sorting은 위 그림과 같이 나온다.
이때, topological sorting의 중요한 특징이 2가지 있는데,
- topological sorting을 진행한 후, 모든 edge들의 화살표 방향은 왼쪽에서 오른쪽으로 나타내야 한다.
- topological sorting은 DAG(Directed Acyclic Graph)에서만 유효하다.
위의 두가지 특징 중 주목해야 될 것은 DAG에서만 유효하다는 점인데, 이 DAG는 이름에서만 봐도 알 수 있듯이, Acyclic 즉, 사이클이 없는 Directed Graph에서만 유효하다는 것이다. 다음 그림을 한 번 살펴보자.

다음 그림과 같은 directed graph에 대해서 DFS를 진행하고, discovery time(빨간색), finish time(파란색)을 표시한 것이다. 이를 이용해 topological sorting을 진행하면, 다음 그림과 같이 나타난다.

위 그림을 자세히 살펴보면, finish time이 큰 순서대로 왼쪽부터 나열했고, 화살표를 나타냈는데, 화살표 하나(c에서 a를 가리키는)가 오른쪽에서 왼쪽으로 향해있다. 이는 topological sorting의 첫번째 특징, 화살표의 방향을 위배하게 된다.
따라서 topological sorting은 순환하지 않는 directed graph, DAG에서만 유효하며, DFS의 finish time을 이용한 정렬 방법이 가장 널리 쓰이는 방식이다.
DFS를 활용한 topological sorting을 좀 더 전문적으로 정의하면 다음과 같다.
Call DFS(G) to compute finish times f[v] for each vertex v.
As each vertex is finished, put it at the head of a list.
Return list.
이렇게 진행하면, list에는 finish time의 역순으로 배열이 정렬되어 있을 것이다.
Topological sorting의 예시로 보았을 때, 모든 vertex들이 explored된 것을 확인할 수 있다. DFS는 이처럼, edge로 연결되어 있지 않더라도, 모든 vertex를 확인하며 진행하기 때문에, DFS tree가 여러개 나타날 수 있다. 이렇게 여러 DFS tree가 나타나져 있는 것을 DFS-forest라고 부른다.
다음 그라프가 주어져 있다고 생각해보자.

위 그라프는 각 수의 배수를 가리킨 directed graph이며, 순환이 나타나지 않는 DAG이다. 위 그림에 대해서 topological sorting을 하기 위해 DFS를 먼저 진행한다면, 다음 그림과 같이 나올 수 있다.

이는, DFS를 vertex 1을 시작점으로 진행한 DFS tree를 나타낸 것이다. 이렇게 되면, 화살표는 생략하고 topological을 나타내면,
1 7 5 3 9 2 6 4 8
이다.
이번에는 vertex 5를 시작점으로 6,7,8,9 순으로 DFS를 진행해보자. 그렇게 되면, 다음 그림과 같은 DFS-forest가 나온다.

이때의 topological sorting을 나타내면
1 3 2 4 9 8 7 6 5
이다.
이렇듯, topological sorting의 결과는 어느 vertex에서 DFS를 시작하느냐에 따라 결과가 달라질 수 있다는 것을 확인 할 수 있다.
5. Partial order and Linear order
집합 S가 있다고 해보자. 이때, 집합 S의 원소들에 대해서 다음 properties가 성립한다
- 만약 x⪯y이고, y⪯z라면, x⪯z이다. (Transitivity)
- 만약 x⪯y이고, y⪯x라면, x=y이다. (Antisymmetry)
- S의 모든 원소 x에 대해, x⪯x이다. (Reflexivity)
여기서 x⪯y라는 것은 "x preceeds or equals y."라는 뜻이다. 즉, x는 y보다 앞서거나 같다라는 뜻인데, 만약 x가 y보다 앞서고 x!=y라면, x≺y라고 하고 다음이 성립한다.
- 만약 x ≺ y이고, y ≺ z라면, x ≺ z이다. (Transitivity)
- 만약 x ≺ y이고, y !≺ x이다. (Antisymmetry)
- S의 모든 원소 x에 대해, x!≺x이다. (Irreflexivity)
x⪯y를 x ≺ y 또는 x=y로 해석할 수 있다.
위의 속성들은 집합 S의 원소의 partial order(예를 들면 x⪯y와 같은 것들)관계를 나타낸 것이다. 이는 Topological sorting에서도 나타나는데, 다음 예시를 한 번 살펴보자.
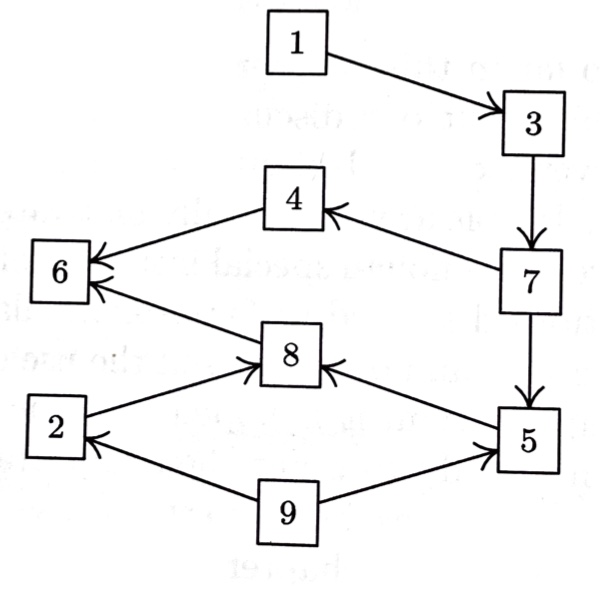
위의 directed graph에 대해서 topological sorting을 진행하고, partial order의 기호로 나타낼 수 있다. 즉, 그라프에서 선행되는 노드들이 위의 기호와 함께 표현될 수 있으며, 이를 만족하는 일렬 정렬이 바로 topological sort 결과이다.

즉, 위의 정리를 통해, topological sorting의 결과도 partial order라는 것을 알 수 있다.
위의 기호들을 이용해 Topological Sorting이 언제 가능한지에 대해서 알아보려고 한다. 4번에서 설명했듯이 조건은 cycle이 존재하지 않아야 한다는 것이다.
만약, directed graph에서 cycle이 존재한다면, 다음과 같은 모순이 생긴다. 예를 들어 x ≺ y ≺ z ≺ x 이러한 관계로 나타낼 수 있는 그라프가 있다면, x ≺ y , y ≺ x가 동시에 나타나게 된다. 이렇듯 모순이 생기기 때문에 topological sorting이 불가능 하다는 것을 알 수 있다. 따라서 다음과 같이 정의할 수 있다.
- DAG는 partial order를 가진다.
- Tolpogical sorting은 주어진 parital order에서 존재 가능한 linear order를 찾는다.
그리고 4번 DFS의 정리 끝쪽에 보면 다음과 같은 정의가 있다고 했다.
- 그라프 G에 cycle이 존재하면, G에 대한 DFS tree는 back edge가 존재한다.
이를 통해 다음을 정의할 수 있다.
- Directed Graph G에 대해 DFS를 진행했을 때, G가 back edge를 생성하지 않는다면, G는 acyclic하다.
6. Correctness of Topological Sort
Directed graph에 대해 DFS를 수행할 때, graph의 edge는 다음 그림과 같이 4가지 카테고리로 분류된다.
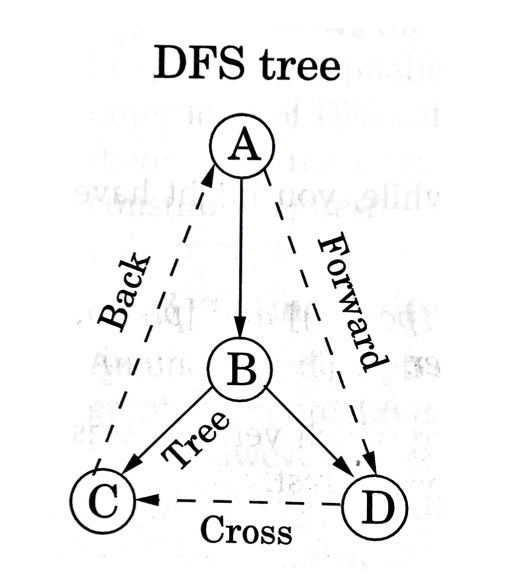
위의 그림에 나타난 edge들에 대해 설명하면,
- Tree edge : 새로운 정점을 처음 방문할 때 사용되는 edge로, DFS tree 또는 forest를 구성하는 edge이다.
- Forward edge : DFS tree에서 조상 노드에서 그 자손 노드로 연결되지만, 직접적인 자식은 아닌 경우의 edge이다.
- Back edge : 현재 정점에서 조상 노드로 되돌아가는 edge이다. 이 edge가 존재하면 cycle이 발생한다.
- Cross edge : 서로 조상-자손 관계가 아닌 정점들 사이의 edge이다.
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Alogrithm_Dijkstra's Shortest Path Algorithm (0) | 2025.06.07 |
|---|---|
| [알고리즘 분석] - Graph Algorithm_Strongly Connected Components (0) | 2025.06.06 |
| [알고리즘 분석] - huffman code (0) | 2025.05.23 |
| [알고리즘 분석] - 분할 정복(divide and conquer) (1) | 2025.04.20 |
| [알고리즘 분석] - 피보나치 (2) | 2025.04.17 |



