이전 글에서는 Graph에 대한 기본 BFS, DFS에 대해서 정리해봤다. 이번 글에서는 이 그라프를 활용한 알고리즘들에 대해서 알아볼 예정이다.
1. Graph의 Connectedness
Graph의 connectedness라는 특징에 대해서 알아보자.
먼저, Connectedness는 말 그대로 연결성이다. 즉, Graph의 vertecies이 서로 연결되어 있으면, 그 graph는 connectedness라는 특징을 가진다는 것이다.
Undirected graph를 생각해보면, edge의 방향성이 존재하지 않기 때문에 vertecies들이 연결만 되어 있다면 connectedness하다는 것을 알 수 있다. 그렇지만 directed graph는 어떨까?
Directed graph에 대해서 알아보자. 다음 예시를 한 번 살펴보면,

a-b-c-d는 서로 reachable한 상태이다. 즉, a,b,c,d를 묶어 하나의 graph로 본다면, directed graph라도 connectedness란 특징이 있다는 것을 알 수 있다.
그렇지만, e를 포함해 a,b,c,d,e를 한 graph로 본다면 어떻게 될까? a,b,c,d에서 e로 도달할 수 있는 방법이 없다. 즉, connectedness란 특징이 없어지게 된다. 이때 우리는 directed graph의 connectedness를 보장하기 위해, a,b,c,d를 components로 가지는 subgraph와 e라는 한 component를 가지는 subgraph로 분류한다.
2. Strongly Connected Componenets(SCC)
다음 예시를 살펴보자.
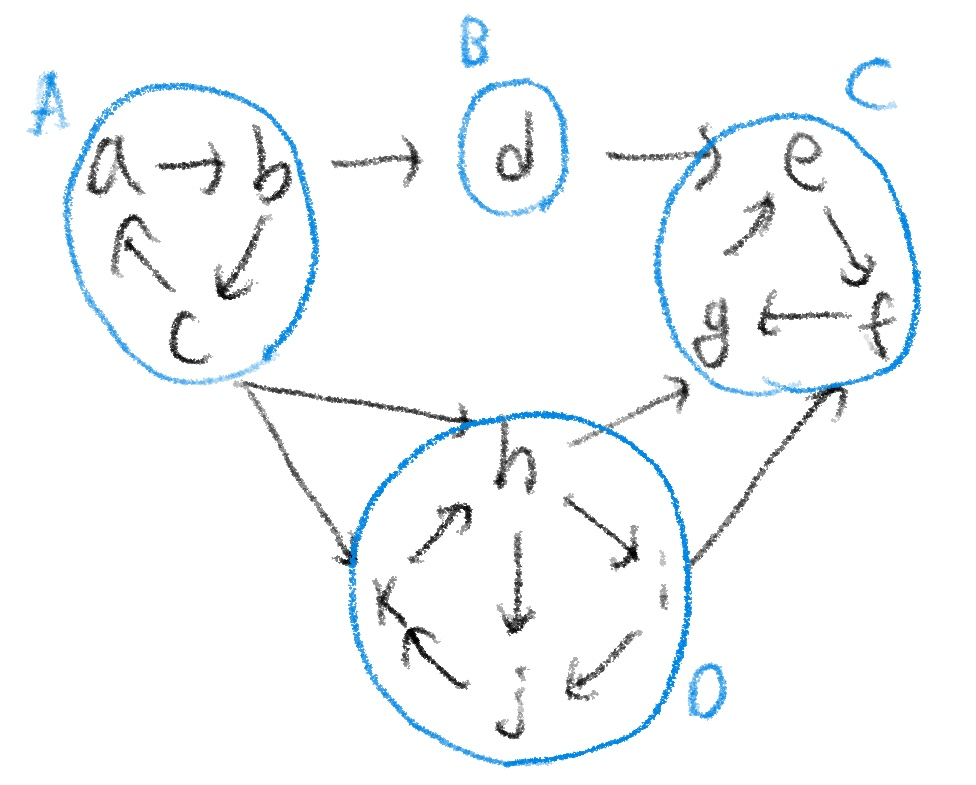
a~k의 vertecies를 가지는 graph를 G라고 하고, G를 connectedness의 특징을 가지는 subgraph인 A,B,C,D로 분류한 graph의 그림이다.
이 때, G의 subgraph의 C를 보면, C는 SCC(Strongly Connected Component) 라고 부른다. SCC는 SCC 내부에 있는 어떤 두 정점을 선택하더라도, 만약 그 두 정점을 u,v라고 한다면
- u에서 v로 가는 경로가 존재하고
- 그 동시에 v에서 u로 가는 경로가 존재하는 경우일 때
그 graph를 SCC라고 부른다. 즉, C의 모든 정점 e,f,g에 대해서 서로를 향한 통로가 동시에 존재한다는 것을 의미한다.
여기서 주목해야될 점은, 현재 만든 모든 subgraph는 one-sided라는 것이다. 즉 한 방향으로만 연결되어 있는 구조라는 점이다. 그 이유는 다음과 같다.
- 예를 들어, 현재는 subgraph A의 vertex b에서 subgraph B의 vertex d로 가는 edge만이 존재하는데,
- 만약 d->b edge가 존재하게 된다면 b와 d는 reachable 상태가 된다.
- 따라서 서로다른 SCC로 분류할 필요가 없어지게 된다.
- SCC는 서로 간의 경로가 존재하면 성립되기 때문에, reachable한 상태가 되는 순간, A와 B는 하나의 SCC로 통합되어야 한다.
따라서 subgraph 간에 경로가 one-sided일 경우에만 서로 다른 SCC로 구분이 가능하게 된다. 따라서 G에 대해서 다음 그림이 성립하게 된다.

이 때, G는 DAG가 된다. 즉, Directed Acyclic Graph가 된다. 이는 다음을 통해 증명할 수 있다.
- 현재, A,B,C,D의 subgraph로 이루어진 G에서 C에서 A로 통하는 새로운 edge를 추가하면,
- A에서 C로 가는 edge와 C에서 A로 가는 edge가 동시에 존재하기 때문에
- A,B,C는 서로 다른 SCC로 구분할 필요가 없어지고,
- 위의 그림이 성립하지 않게 된다.
결론은 SCC간에 cycle이 존재하게 되면 더 이상 서로 다른 SCC가 아니게 되므로, SCC 사이에 형성되는 graph는 본질적으로 사이클이 없는 DAG가 될 수 밖에 없다.
3. Kosaraju's Double DFS Algorithm for SCC
위와 같은 graph를 처리하기 위한 알고리즘도 존재하는데 이 알고리즘을 바로 Kosaraju's Double DFS 알고리즘이라고 부른다. 이름에서 알 수 있듯이, 2번의 DFS를 이용하여 graph를 컴퓨터 상에서 처리하는 것이다. 먼저, 수도코드를 확인해보자.
DFS(G^T) to compute the finish times f[v] for each vertex
DFS(G) in decreasing order of f[v]
Component trees of DFS-forest are the SCC's of G
위의 코드 순서대로 진행되는데, 과정을 더 자세히 알아보자.

위 그라프에 대해 Kosaraju's Double DFS 알고리즘을 적용하면 다음과 같다.
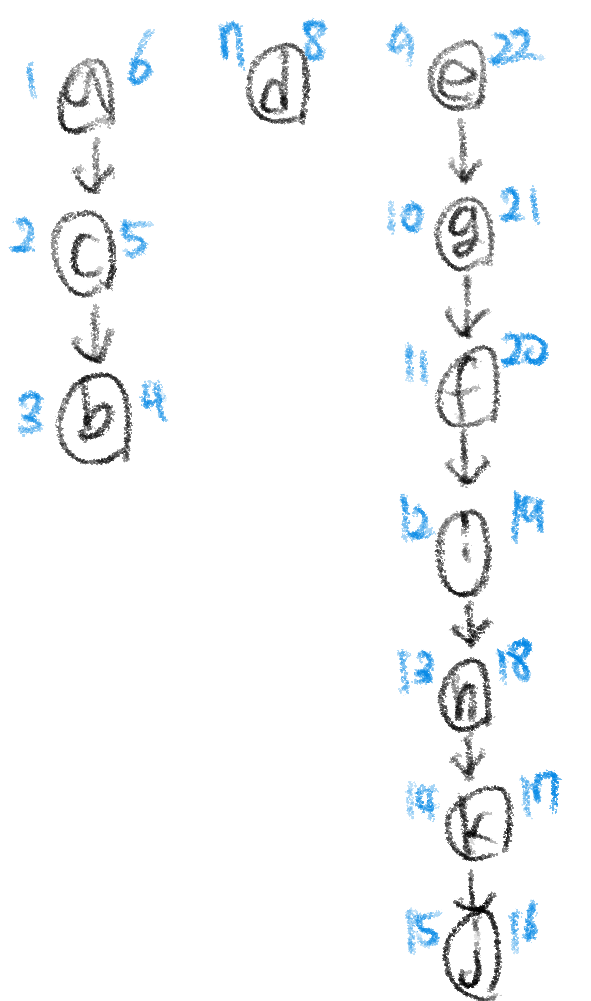
위 그림은 DFS(G^T)를 실행한 결과이고, 이 실행결과에 파란색 숫자로 discovery time과 finish time을 기록한 것이다. 이 실행결과에 대한 finish time을 f[v]라고 하면, 다음 DFS(G)는 f[v]가 감소하는 순서대로 진행한다. 다음 그림을 확인해보자.

즉, f[v]가 제일 큰 순서대로 G에 대해서 DFS를 실행한 결과이다. 위 그림이 최종적인 G의 DFS-forest가 된다.
그럼 이 순서로 알고리즘을 실행하는 이유는 무엇일까?
- DFS(G^T)에 대한 f[v]를 이용해 DFS(G)를 이용하게 되면 G의 DFS-forest를 SCC에 따라 얻을 수 있는데,
- 만약, f[v]를 이용하지 않고 DFS(G)만 진행하게 된다면
- 예를 들어 G의 e에서 시작해야되지만, i에서 시작한다면
- subgraph SCC인 D의 component를 다 찾지 못하고 f로 이동하는 경우가 생기고
- 이렇게 되면 SCC별로 구별된 G의 DFS-forest를 얻지 못하게 된다.
결과적으로, 위의 알고리즘을 순서대로 수행함으로써, 우리는 SCC별로 정확하게 구분된 DFS-forest를 얻을 수 있다.
이는 각 DFS 트리가 하나의 Strongly Connected Component를 나타내며, 전체 그래프 구조를 컴퓨터 상에서 명확하게 분해하고 분석할 수 있게 해준다.
4. Source vertex와 Sink vertex
DAG에서는 source vertex와 sink vertex가 존재하게 되는데, 먼저 이들에 대해서 정리해보면 다음과 같다.
- Source vertex : 본인을 향해 들어오는 edge가 없는 vertex
- Sink vertex : 나가는 edge가 없는 vertex
이들은 G의 SCC로 나눈 A,B,C,D에 대해 topological sorting을 이용하면 쉽게 찾을 수 있다.

위 그림에 대해서 topological sorting을 해보면, 다음과 같이 나타낼 수 있다.

이 그림에서 sink vertex는 C임을 알 수 있고, source vertex는 A임을 알 수 있다.
이렇게 sink vertex와 source vertex를 찾으면 어떻게 될까?
Kosaraju 알고리즘을 이용할 때, 두 번째 DFS를 실행하면, C에서 시작함을 알 수 있다. C가 sink vertex이기 때문에 다른 vertex로 이동할 경우가 생기지 않고, 이렇게 되면 우리는 원하는 DFS-forest에 한 걸음 더 가까워진다.
그 다음은 B나 D에 대해서 실행되게 되는데 D에서 C로 나가는 vertex, B에서 C로 나가는 vertex가 있기 때문에 어느 쪽에서 시작하던 원하는 DFS-forest를 얻을 수 있다는 것은 자명하다.
따라서 sink vertex와 source vertex의 개념을 이용해 Kosaraju 알고리즘이 진행된다는 것을 알 수 있다.
+) Kosaraju 알고리즘은 2번의 DFS를 이용하기 때문에 linear time 알고리즘이다:)
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Algorithm_Floyd's Algorithm for All-Pairs Shortest Paths (1) | 2025.06.13 |
|---|---|
| [알고리즘 분석] - Graph Alogrithm_Dijkstra's Shortest Path Algorithm (0) | 2025.06.07 |
| [알고리즘 분석] - Graph Algorithm_BFS, DFS (1) | 2025.06.06 |
| [알고리즘 분석] - huffman code (0) | 2025.05.23 |
| [알고리즘 분석] - 분할 정복(divide and conquer) (1) | 2025.04.20 |



