이전 글에서는 SCC(Strongly Connected Component)와 그에 대한 알고리즘 기법인 Kosaraju's Double DFS Algorithm에 대해서 정리해 보았다.
이번에는 그라프 알고리즘 중에서 컴퓨터 네트워크의 라우팅에서 잘 활용되고 있는 Dijkstra's shortest path 알고리즘에 대해서 정리해보려고 한다.
1. 다익스트라 알고리즘 프롤로그
이전에 BFS에 대해서 정리할 때, 임의의 두 정점에 대한 최단경로를 구하는 알고리즘에 대해서 알아보았다. 다익스트라 알고리즘은 임의의 두 정점이 아닌, 그리고 weighted(가중치)가 존재하는 그라프에 대해서 조금 더 general한 문제에 대한 해결책을 제시한다.
이 알고리즘은 BFS의 주변 정점 탐색기법을 활용하기 때문에 이 자체로 BFS의 일반화된 버전이라고 여겨진다. 이 알고리즘은 source로 부터의 거리를 기억하기 위해 BFS의 queue를 이용하는 방식을 priority queue를 이용하는 방식으로 구현한다.
2. 다익스트라 알고리즘
위에서 설명한 다익스트라 알고리즘은 그럼 어떻게 진행될까? 수도 코드를 따라 정리해 볼 예정인데, 다음 전제 조건들이 있다.
- s : 시작 지점
- T : shortest-path tree(초기값은 empty)
- main Loop의 재귀는 u를 T에 추가한다.(이때 u는 T 밖에있는 s와 가장 가까운 vertex이다.)
다음 수도 코드를 확인해보자.
s: given starting vertex
Q: priority queue (of vertices v's with key d[v])
(T: growing shortest-path tree whose vertices = V-Q)
Init:
for each vertex v
d[v] <- infty // inititally set as infinity
push(v) // Assume d[v] is the priority.
d[s] <- 0 // Also, if d[] is changed,
// priority queue is adjusted appropriately.
Main Loop:
while Q is not empty
u <- pop() // The first one is s!
for each neighbor v (in Q) of u
if(d[u]+w(u,v) < d[v]) // if newly added vertex u makes v closer
d[v] <- d[u] + w(u,v) // update the distance (which updates Q)
parent[v] <- u // u is added to T
Output:
return parent[] // the shortest-path tree
먼저, s는 전제 조건에서 말했듯, 시작 vertex이고, T는 shrotest-path tree이다.
따라서 Init, 즉 초기값을 모든 정점 v에 대해서 d[v] = ∞ 로 초기화하고, Q에 push한다. 그리고 d[v]는 s로부터 정점 v까지의 현재까지 알려진 최소 거리를 의미한다. 따라서 d[s] = 0으로 초기화한다.
이제 Main Loop으로 이동해서,
- Q(현재 q에 모든 정점이 infinity로 존재하는 상태)에서 한 정점 u를 pop한다.(최초에는 s가 pop된다.)
- 그리고 이제, s의 이웃들 u에 대해서(이때 v는 아직 Q에 있는 상태) 다음 조건을 확인한다.
- if (d[u] + w(u,v) < d[v]),
- 즉, (초기값 s에서 u까지의 거리) + (u에서 v까지의 거리) < (초기값에서 v까지 거리)를 만족한다면, d[v]값을 d[u] + w(u,v)로 갱신한다.
- 그리고 v의 parent를 u로 기록하며 이때 u가 T에 포함된다.
그리고 마지막에, Ouput 부분은 기록한 parent를 return 하며 가장 짧은 경로의 tree를 만든다.
그럼 이때 생기는 궁금점은 u가 어떤 기준으로 선택되는 것이냐이다. 이 질문에 대한 해답은 다익스트라 알고리즘은 greedy algorithm(탐욕 알고리즘)이라는 것에 있다.
초기화 단계에서는
- 모든 정점 v의 거리를 d[v] = ∞로 설정하고,
- 시작 정점 s만 d[s] = 0으로 초기화한다.
- 그리고 각 정점은 우선순위 큐(Q)에 push()된다. 이때 우선순위는 d[v] 값으로 정해진다.
탐욕 알고리즘이란 앞서 정리했지만 간단히 요약하면 매 순간 최선의 선택을 하는 방식이다.
- Huffman 코드에서 가장 빈도수가 작은 두 노드를 반복적으로 선택하여 트리를 만들었듯이,
- 다익스트라 알고리즘도 현재까지 가장 가까운 정점을 반복적으로 선택한다.
따라서
- 가장 먼저 d[s] = 0인 시작 정점 s가 pop되고, 이웃들의 d[v] 값이 갱신되며 parent[v]도 설정된다.
- 이후에는, 갱신된 거리들 중에서 가장 짧은 값을 가진 정점이 다음에 pop된다.
- pop된 정점은 최단 경로 트리 T에 포함되고, 그 이웃들에 대해 같은 과정을 반복한다.
정리하자면, 다익스트라는 가장 가까운 정점부터 pop해 나가는 greedy algorithm의 한 종류이며, 이 방식을 통해 각 정점은 자신에게 도달하는 최단 경로가 확정된 상태로 큐에서 pop된다.
다음 예시를 한 번 살펴보자.
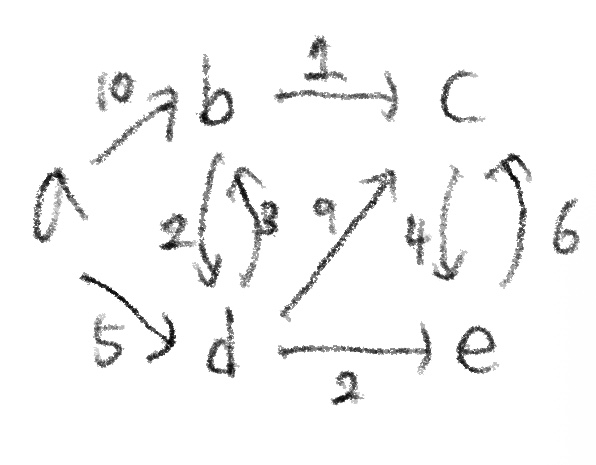
이때, 위의 그라프를 해당 수도코드를 통해 진행한다고 하면, 진행과정은 다음과 그림처럼 나타난다.

그림에 대해서 설명하면,
- 초기에 처음 정점 a 제외 모든 vertex들을 Q에 push하며 d[v]값을(파란색) 무한대로 초기화한다.
- a를 pop()한 뒤, a의 이웃인 b와 d의 d[v]값을 각각 10,5로 갱신한고 b,d의 부모를 a로 설정한다. 그 후, a는 T에 포함된다.
- Q에서 다시 가장 짧은 값인 5를 가진 d를 팝하고, d의 이웃인 b,c,e의 d[v]값을 계산한다.
- 이때, b는 이미 a의 이웃으로 10이라는 값을 가졌지만, a-d-b로 가면 8로 d[v]값이 줄어들었기 때문에 8로 갱신하고, parent도 기존의 a에서 d로 갱신한다.
- 이 과정을 반복하며 Q가 empty가 될때까지 T의 트리 구조를 만든다.
그렇다면 이 다익스트라 알고리즘의 시간복잡도는 어떻게 될까? n개의 정점과 m개의 edge에 대해서 다익스트라 알고리즘을 진행한다고 가정해보자.
heap으로 구현된 우선순위 큐를 생각해보면, 키값은 완전이진트리로 구성되어 있다는 점을 참고하자. 따라서 우선순위 큐에 push하고 pop하는 경우는 모두 O(logn) 시간이 걸리는 것을 알 수 있다.
먼저 Init 단계에서, heap에 n개의 정점을 push하는 시간은 O(nlogn)이다.
그 후, Main Loop 단계에서 n개의 정점을 각각 pop하는 시간도 O(nlogn)이다. 또, for 문 안의 d[v] 값을 갱신하는 경우를 생각해보자. 이때, key 값을 갱신하는 시간은 완전 이진 트리 구조에서 자리를 찾는 시간으로, O(logn)시간이 걸린다. 그런데 이 과정이 최대 edge 갯수만큼 일어나기 때문에, O(mlogn)시간이 걸린다.
따라서 다익스트라 알고리즘의 시간복잡도는 O((n+m)logn)이다.
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Algorithm_Floyd's Algorithm for All-Pairs Shortest Paths (1) | 2025.06.13 |
|---|---|
| [알고리즘 분석] - Graph Algorithm_Strongly Connected Components (0) | 2025.06.06 |
| [알고리즘 분석] - Graph Algorithm_BFS, DFS (1) | 2025.06.06 |
| [알고리즘 분석] - huffman code (0) | 2025.05.23 |
| [알고리즘 분석] - 분할 정복(divide and conquer) (1) | 2025.04.20 |



