분할 정복 알고리즘
분할 정복 알고리즘은 이제 처음 배울 알고리즘 방식이다. 분할 정복 알고리즘은 제목에서도 알 수 있듯이, divde와 conquer하는 방식이다. 그리고 이 알고리즘에서 중요한 것은 바로 reqursively하게 진행된다는 점이다. 즉, 재귀적으로 divde와 conquer하는 방식인 것이다. 사실 이 방법에서 더 중요한 것은 divde and conquer 방식이 아닌 recursive가 더 중요한 것이다. 즉 재귀가 더 중요한 알고리즘이라고 알아두고 자세히 알아보자.
1. School Arithmetic
첫 번 째로 알아볼 방식은 school arithmetic 방식이다. 이 방식은 무엇이냐면, 우리가 학교에서 흔히 배웠던 곱셈 방식이다. 덧셈을 먼저 알아보자.

위 그림은 1234 + 5678을 학교에서 배운 방식으로 진행한 그림이다. 각 자릿수마다 덧셈을 진행해주고 carry값이 발생하면 다음 자릿수에 캐릿값을 더해주는 방식이다. 4자릿수 덧셈에 대해 기본적으로 4번의 덧셈에 캐릿값 2번이 발생해 총 6번의 덧셈이 진행됐다. 덧셈에서는 그럼 총 몇 번의 덧셈이 발생할까? 일반화를 해보자.
2개의 n 자릿수를 더해준다고 생각을 해보자. 이 때, 기본적으로 n자리 덧셈이기 때문에 n번의 덧셈이 발생하고, 캐릿값은 일의 자리수 빼고 모든 자릿수에서 발생할 수 있기 때문에 최대 n-1번이 발생할 수 있다. 따라서 n자릿수 덧셈을 할 때, 최대 발생할 수 있는 덧셈 횟수는 2n-1번임을 알 수 있다.
이제는 곱셈에 대해서 알아보자. 똑같이 1234 * 5678을 계산을 해 볼 예정이다.

우리가 학교에서 배운 방식은 각 자릿수마다 곱셈을 진행한 것이다. 1234 * 5678을 예시로 들면, 8과 1234를 곱해주고, 7과 1234를 곱해주고 6 * 1234, 5 * 1234를 진행해주고 더해주는 방식이다. 이렇게 곱셈에서는 곱셈과 덧셈이 복합적으로 이뤄진다. 그럼 곱셈과 덧셈중에 더 복잡한 것은 무엇일까? 곱셈이다. 왜 그럴까?
만약 n자릿수 두 수를 곱한다고 가정을 하자. 그럼 곱셈은 총 몇 번, 덧셈은 총 몇 번이 일어날까? 아래 그림을 참고해보자.

n 자릿수 곱셈을 한다고 치면, 기본적으로 총 n 번의 곱셈과 그 n번의 곱셈이 n번 발생하므로 총 n^2번이 일어난다. 그리고 일의 자릿수 곱셈 결과와 십의 자릿수 곱셈 결과를 더해줄 때, 기본적으로 n-1번의 덧셈과 최악의 경우 캐릿값을 고려하면 n-2번, 총 2n-3번에, 이 과정이 n번 발생하므로, 2n^2-3n번이 발생한다. 그래서 곱셈의 시간 복잡도는 O(n^2)이 된다.
아래 삼각형의 의미는, 덧셈의 횟수인데, 가운데 자리 근처에서 최대 n번의 덧셈이 발생하고 최고 자릿수나 최저 자릿수로 갈수록 덧셈횟수는 1씩 감소한다. 그럼 위 삼각형과 같이 덧셈횟수를 표현할 수 있는데, 밑변은 2n, 높이는 n이기 때문에 덧셈횟수는 n^2임을 알 수 있다. 이도 시간 복잡도는 O(n^2)으로 표현할 수 있다.
그렇다면 곱셈은 항상 O(n^2)으로 표현될까? 그렇지 않다. 더 좋은 방법이 존재한다. 바로 카라츠바 방법이다.
2. Karatsuba Method(카라츠바 방법)
카라츠바 방법은 무엇일까? 자릿수를 반으로 나눠서 곱셈을 진행하는 방식이다. n 자릿수 U, V에 대해 곱셈을 진행해보자.

앞의 n/2 자릿수를 각각 U1, V1 나머지 n/2 자릿수를 U0, V0라고 하고 곱셈을 진행해보면 아래와 같은 식이 나온다.

이대로 곱셈을 진행하게 되면, 우리가 배웠던 school arithmetic 방식과 시간복잡도가 차이가 없다. 그 이유는 카라츠바 방법을 다 설명하고 얘기해보도록 하겠다. 그럼 여기서 카라츠바 방법은 어떻게 바뀔까? 가운데 U1V0 + U0V1을 다음과 같이 정리한다.
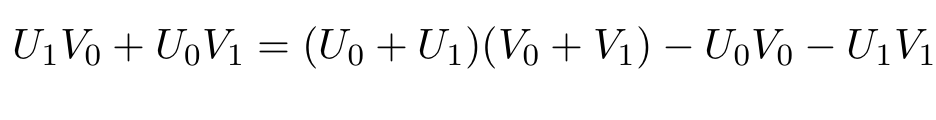
위와 같이 정리하게 된다면, (U0+U1)(V0+V1)에 대한 곱셈만 한 번 더 진행되고, U0V0, U1V1은 앞선 UV에서 이미 구한 값이므로, 전체적인 UV 값을 구하기 위해서는 총 3번의 곱셈이 나타난 것을 알 수 있다. 이제 1234 * 5678을 카라츠바 방법으로 진행해보겠다.

먼저, 위 그림과 같이 앞, 뒤 각각 2자리로 나누고, 다음과 같이 곱셈을 진행한다.
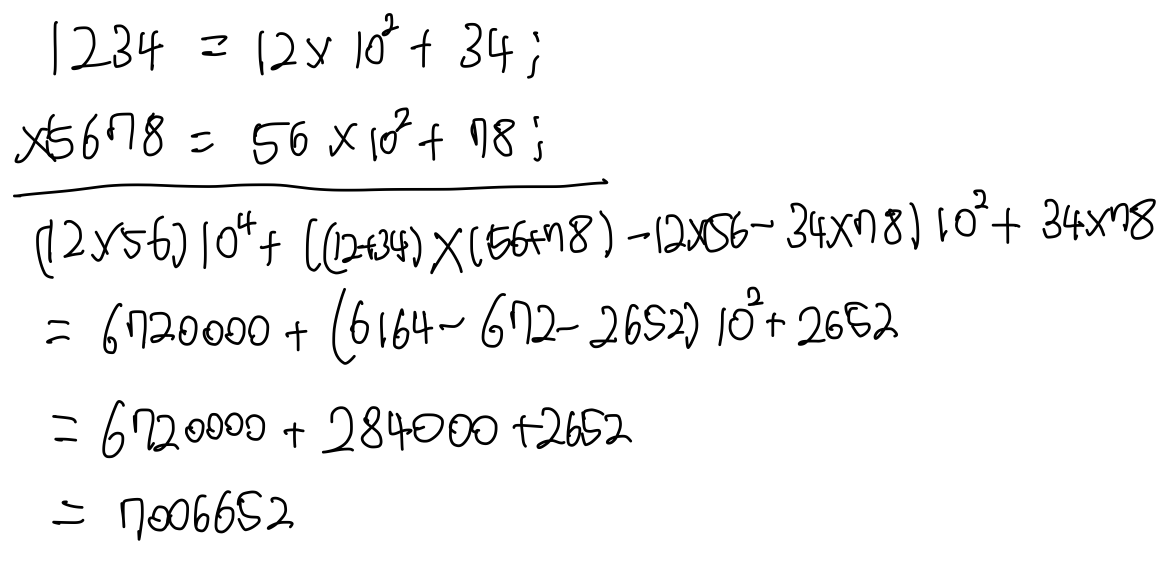
카라츠바 방법으로 진행한 곱셈은 위와 같이 나타난다.
그럼 이제 이 카라츠바 방법을 수도코드로 작성해보자.
mult(u,v)
{
if both u and v one-digit numbers
return u*v;
else
u1, v1 <- first n/2 digits
u0, v0 <- remaining n/2 digits
uv1 <- mult(u1, v1)
uv0 <- mult(u0, v0)
w <- mult( (u1+u0) , (v1+v0) ) - uv1 - uv0
return uv1*10^n + w*10^(n/2) + uv0;
}
위와 같이 수도 코드를 작성할 수 있다. 위 수도코드를 보면 알 수 있듯이, 총 3번의 mult()함수가 mult()함수 내부에 recursive하게 불렸고, 위의 카라츠바 방법을 따른 수도코드이다.
이 수도코드를 보면 알 수 있는 점은 2개의 n자릿수 곱셈을 하기 위해 3번의 mult()재귀가 발생했다는 점이다. 그럼 예를 들어 n자리 2수를 곱한다고 치면 아래와 같은 재귀 트리가 나온다.

재귀 트리에 대해 설명하면,
1. 각 수를 n/2자릿수로 분할하고,
2. n/2자릿수 3번의 곱셈을 위해 mult()를 3번을 호출하고
3. 곱한 숫자를 합치는 과정
이다.
재귀트리에 3번 과정은 나타나지 않았지만, 1,2 번 과정은 잘 나타나있다. 그럼 이를 이욯해서 카라츠바 방법의 시간복잡도를 구해보자.
재귀 트리에서 맨 처음에 일을 진행하는데 걸리는 시간을 T(n)이라고 하자. 예를 들면, 마지막에는 T(1) = 1 인 것이다. 그럼, T(n) 에서 T(n/2)로 진행될 때 걸리는 시간은 얼마나 될까?
그 전에 재귀트리의 height, 높이를 먼저 구해보자. 재귀트리가 1, single-digit-multiplication까지 가는데 반복횟수를 k라고 하자. n/2^k이 1이 될 때까지 이 과정을 반복하기 때문에 k = lg(n)일 때까지 반복한다. 따라서 이 재귀트리의 높이는 lg(n)임을 쉽게 알 수 있다.
위의 1,2,3번을 고려하면 된다. 각 수를 n/2자릿수로 분할하는 과정과 곱한 숫자를 합치는 과정은 linear time이고 3번의 n/2자릿수 곱셈은 3*T(n/2)이 걸린다. 즉 T(n) <= 3T(n/2) + Cn이다. linear time에 C라는 상수가 붙은 것은 알고리즘 구현 방식 등에 의해 달라지기 때문이다. 그럼, T(n/2) 에서 T(n/4)로 진행될 때는, T(n/2) <= 9T(n/4) + C(n+ 3*(1/2)n) 이다.
다음 그림을 보면 더 직관적으로 이해할 수 있다.

트리의 높이가 앞서 구했듯, lgn, 반복횟수도 이와 같기 때문에 1이 될 때까지 lgn 번을 반복하게 되고, T(1)일 때, 위의 마지막 식과 같이 구해진다. 이를 좀 더 정리하면 다음과 같은 카라츠바의 시간 복잡도를 구할 수 있다.
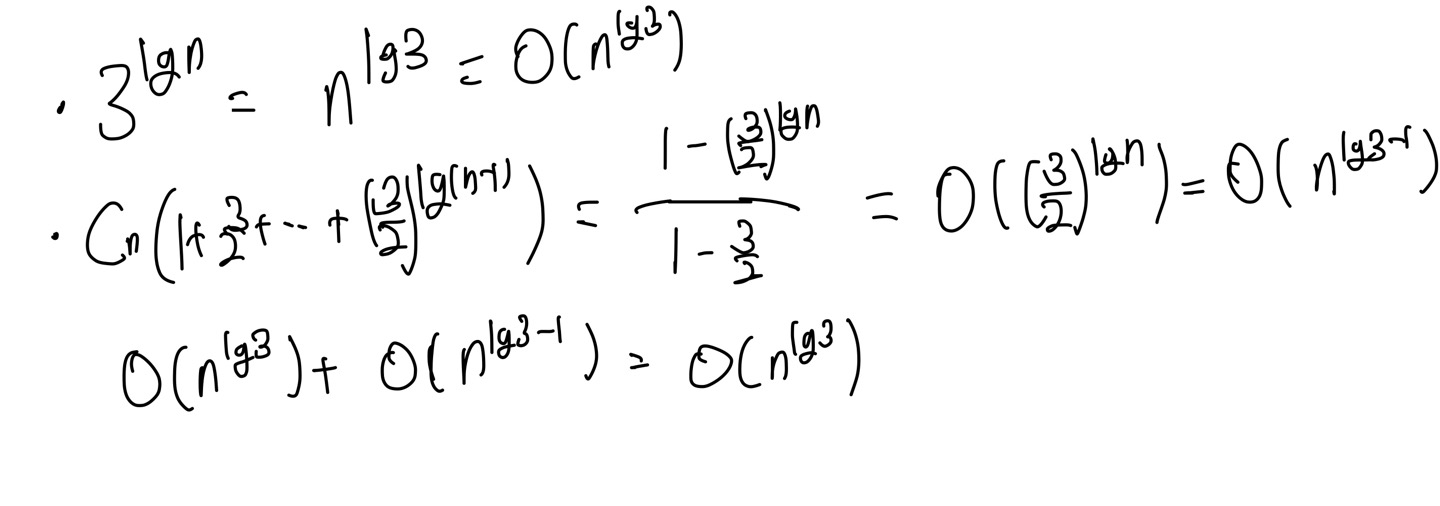
따라서 카라츠바의 시간 복잡도는 O(n^(lg3))임을 알 수 있다.
-카라츠바 방식의 응용
카라츠바 방법은 1960년 대에 나온 divde and conquer 알고리즘이다. 그 후에 이 방법을 좀 더 일반화시킬 수 있었다. U와 V를 k 파트들로 쪼개는 방식이다. 이렇게 쪼개게 되면, 총 2k-1번의 재귀콜이 생기게 되고, 카라츠바 방식과 동일하게 시간 복잡도를 구할 수 있게 된다.
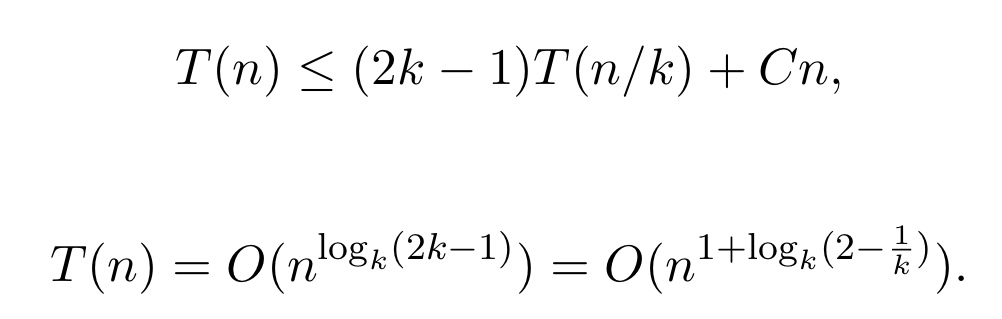
위와 같이 시간 복잡도가 나옴을 알 수 있다.
만약 k가 점점 커진다면 이론적으로는 시간 복잡도가 O(n)과 가깝게 되긴 하지만, 절대 O(n)이 될 수는 없다. 즉, k가 점점 커짐에 따라 시간 복잡도는 O(n^(1+ ε))이 되고, ε>0인 아주 작은 양수이다. 그 이유는 n자릿수 곱셈에는 최소 O(n)이라는 정보량이 필요하고 변환 과정에서 추가적인 시간이 필요하기 때문이다.
+) 행렬 곱셈에 대해서
n*n 행렬 곱셈에 대해서 일반적으로 n^3시간이 걸린다. 다음 기사에서는 O(n^lg7)을 시작으로 점점 O(n^2)으로 가까워지고 있다는 것을 보여주고 있다. 그렇지만 행렬 곱셈은 절대 n^2이 될 수 없다. 그 이유는 모든 원소 한 번씩은 읽어야 되므로 최소 n^2의 시간이 필요하기 때문이다. 그저 n^2으로 가까워져 가고 있을 뿐이다.
https://www.quantamagazine.org/new-breakthrough-brings-matrix-multiplication-closer-to-ideal-20240307/
New Breakthrough Brings Matrix Multiplication Closer to Ideal | Quanta Magazine
By eliminating a hidden inefficiency, computer scientists have come up with a new way to multiply large matrices that’s faster than ever.
www.quantamagazine.org
-카라츠바 방법 정리
곱셈의 계산에 있어서 카라츠바 방법이 항상 빠르다는 대답에는 No라고 말해야 될 것이다. 적당히 큰 수에 대해서는 학교에서 배운 곱셈의 방식이 더 빠르다. 그 이유는 카라츠바는 덧셈 뺄셈을 일반 곱셈보다 많이 하는 방식인데, 이 덧셈/뺄셈시간에 재귀 호출시간이 적당히 큰 수에 대해서는 그냥 곱셈에 비해 시간이 더 오래 걸리기 때문이다. 그렇지만, 여전히 엄청 큰 수에 대해서는 카라츠바가 더 빠른 편이다.
3.Binary Search(이분 탐색)
자료구조 시간에 배운 이분 탐색도 재귀가 일어나는 탐색이라는 것을 알 수 있다. 기억이 안날 수 있으니 다음 수도 코드를 간단히 보자.
binsearch(K,l,u,x)
{ // size of list : n = u-l+1
if(l>u)
return -1
m = floor((l+u)/2)
if K[m] = x
return m
else if K[m] < x
return binsearch(K,m+1,u,x)
else
return binsearch(K,l,m-1,x)
} 위 수도 코드를 보면 알 수 있듯이 분명하게 재귀 콜이 일어남을 알 수 있다. 그럼 이 이분탐색에 대해서 시간복잡도를 구해 보자.
n개의 key 값에 대해서 이분 탐색을 진행한다고 하고, T(n)을 시작이라고 하면 이분 탐색의 재귀호출 트리는 다음과 같다.

재귀 호출은 한 번씩 일어나며 찾고자하는 키값과 비교해 진행하게 된다. 재귀 호출 함수의 높이는 lgn이 되고, 한 번 일이 진행될 때, 걸리는 시간은 최대 T(n/2)에 키값을 비교하는 시간 C를 더한 값이다. 따라서 이 이분 탐색을 반복하게 되면 시간 복잡도는 O(lgn)이 됨을 알 수 있다.
4. Merge Sort(병합 정렬)
이제 자료구조 시간에 배운 병합 정렬에 대해서도 알아보자. 자료구조 시간에 배운 여러 정렬 알고리즘 중, merge sort와 quick sort가 divde and conquer 알고리즘에 해당한다. 병합 정렬도 재귀 콜이 일어남을 다음 수도 코드를 통해 알 수 있다.
mergesort(A(l..r))
{
if(l<r)
m = (l+r)/2
mergesort(A(l..m))
mergesort(A(m+1..r))
merge(A(l..m),A(m+1..r))
}
병합 정렬은, 자료구조 시간에도 배웠듯이, merge에서 대부분의 일이 일어난다. 값을 비교하고, 합치는 과정이 merge안에 나타나져 있는데, merge에 대한 코드를 한 번 확인해보자.
merge(A[l..m], A[m+1..r])
{
copy A[l..r] into B[l..r]
i <- l
j <- m+1
k <- l
while (i<=m and j<=r)
if (B[i]<=B[j])
A[k++] <- B[i++]
else
A[k++] <- B[j++]
//나머지 부분 merge 하기
if (i>m)
while (j<=r)
A[k++] <- B[j++]
else
while(i<=m)
A[k++] <- B[i++]
}
코드에 대해 간단히 설명하면, 합칠 배열에 대한 buffer를 만들고, 배열 B에서 비교를 한 뒤, 작은 값부터 차례대로 A에 다시 집어 넣는 것이다.
이 때, merge 과정에서 m과 n의 배열을 합친다고 가정해보자. 그럼 key값 비교는 최소 min(m,n)번, 최대 m+n-1번이 일어나는 것을 알 수 있다. 그리고, 이 때, 버퍼에 옮겼다가 다시 원래 배열로 옮기는 시간은 2(m+n)이다. 따라서 merge과정의 시간 복잡도는 O(m+n)임을 알 수 있다.
그럼 이제, 본격적으로 merge sort에 대한 시간복잡도를 구해보자. T(N)을 mergesort()의 실행시간이라고 하면, T(N)은 다음 식을 만족한다.

즉, N/2개의 배열로 나누고, 배열을 합치는 시간 N이 걸리는 것을 표현한 것이다. 똑같이, 2T(N/2)=4T(N/4)+CN으로 표현할 수 있고 T(N)을 T(1)에 대한 식으로 표현하면 다음과 같다.
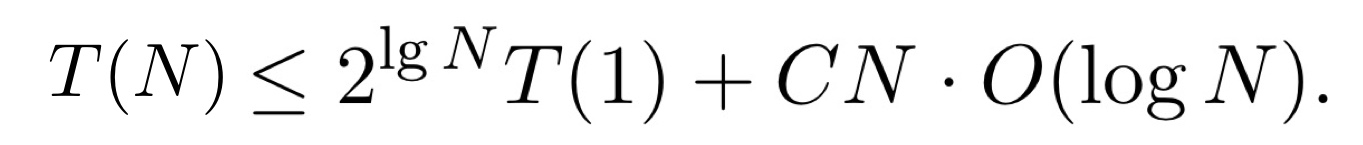
따라서 merge sort에 대한 시간 복잡도는 O(NlogN)임을 알 수 있다.
Merge sort에 대해서 정리해 보자면, merge sort는 배열을 N/2로 쪼개는 것이므로 이진 트리형태로 나타남을 알 수 있다. 따라서 N개의 input에 대해서는 N개의 leaf-node와 N-1개의 internal node가 생긴다는 것을 알 수 있다. 그렇기 때문에 총 재귀 호출 횟수는 2N-1번이 일어난다.
5. Quick Sort
자료구조 시간에 배웠던 quick sort도 divde and conquer 방식에 해당한다. quick sort의 코드를 먼저 살펴보자.
quicksorkt(A[l..r])
{
if(l<r)
p<-partition(A[l..r]) //==> A[l..p-1]A[p]A[p+1..r]
quicksort(A[l..p-1])
quicksort(A[p+1..l])
}
mergesort에서 merge()함수가 거의 모든일을 했듯이 quicksort에서는 parition()함수가 거의 모든 일을 한다고 생각하면 된다. partition은 다음과 같은 순서로 진행한다.
- 배열의 맨 첫번째 값을 pivot으로 설정하고,
- A[l..r]의 배열을 A[l..p-1]A[p]A[p+1..r]로 재배열한다.(A[p] 왼쪽은 p보다 작은 값들로, 오른쪽은 큰값들로 재배열)
예를 들면 다음과 같다. 입력 배열이 [3,9,1,6,5,2,7]이라고 가정하면 다음과 같이 진행된다.

parition 함수에서는 pivot을 나머지 수와 비교하는 과정이 포함되기 때문에 linear time이 걸린다. 즉, N개의 input이 들어오면, pivot을 설정하고 pviot과 n-1번의 비교가 진행되기 때문에 시간 복잡도는 O(n)이다.
자료구조에서 quick sort의 시간 복잡도는 O(nlogn)이고, 최악의 경우 O(n^2)의 시간이 걸릴 수 있다고 배웠다. 그 예시는 대표적으로 input이 정렬되어 있는 배열로 들어오는 경우이다. 다음 그림을 살펴보자.
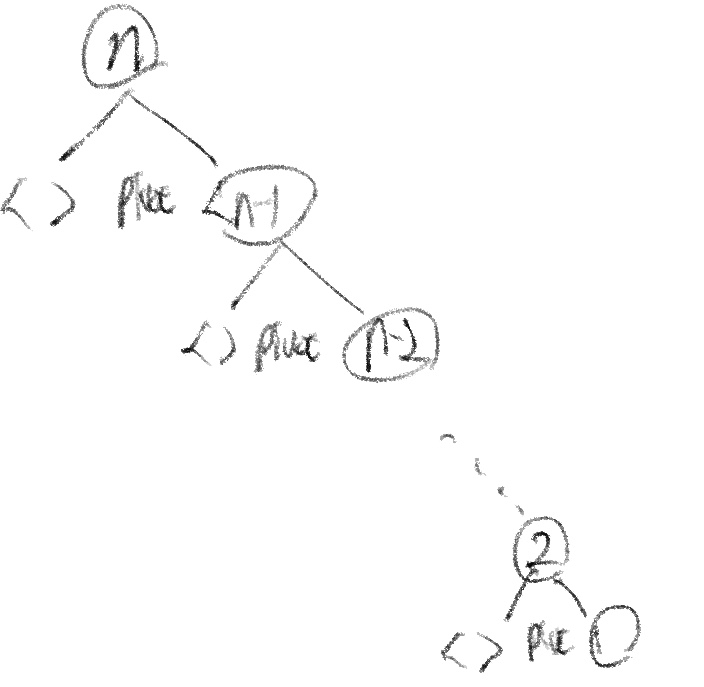
즉, 각 단계별로 n-1번의 비교, n-2번의 비교.. 가 일어나게 되고, 이 비교횟수를 다 더하면 n^2으로 나타나기 때문에 시간 복잡도가 O(n^2)이 된다.
그럼에도 불구하고, quick sort의 시간 복잡도를 O(nlogn)으로 표현하는 이유는 무엇일까? quicksort의 실행시간을 T(n)이라고 하자. 그리고 쪼개지는 배열의 한쪽 크기를 α라고 하자. 그럼 T(n)을 다음과 같이 표현할 수 있다.

T(n)을 T(αn)+T((1-α)n)으로 쪼개고 pivot과 키값 비교하는 linear time인 Cn의 합으로 나타낼 수 있는 것이다. 이 때, α가 1/2이라면, 즉 정확히 예쁘게 반으로 쪼개진다면, T(n)은 merge sort와 똑같은 식으로 표현되기 때문에 시간 복잡도는 O(nlogn)으로 표현할 수 있다.
그럼 α가 1/2이 아닌 다른 값을 가지면 어떻게 될까? α=2/3이라고 하자. 그럼 다음과 같이 트리를 나타낼 수 있다.

이 트리의 높이는 그림에 나타나져 있듯이 밑이 3/2인 로그 n의 값을 가진다. 그리고 각 단계의 실행시간은 쪼개진 배열들의 각 pivot과 키값들을 비교하는 것인데, linear time으로 Cn임을 알 수 있다. 따라서 α가 2/3일 때도 시간 복잡도는 O(nlogn)임을 알 수있다.
>로그 밑이 상관 없다는 것은 알고리즘 맨 처음 정리글을 참고하자.
cf. quick sort는 최악의 경우(정렬된 배열 입력값)를 제외하고는 α가 어떤 값을 가져도 시간 복잡도는 O(nlogn)이라고 할 수 있다. 그럼 왜 O(nlogn)이 quick sort의 대표 시간 복잡도가 됐을까?
증명이 아닌 간단하게 설명만 하고 넘어가자면, 최악의 경우의 수가 나올 때는 N개의 key값이 트리에서 한 쪽 방향으로만 뻗어가는 경우이다. 트리를 생각하면 N개의 key 값은 갈 수 있는 경우는 left-subtree 쪽이거나 right-subtree쪽이다. N개의 input이 한쪽으로 치우치는 경우의 수는 2^n이 되는 것이다.
그렇지만 이 때, N개의 input이 항상 최악의 경우가 생기는 것은 아니다. 즉, 무작위 배열로 들어오는 경우의 수는 N!임을 알 수 있다. 이 때, N!은 황금비율로, 2^n보다 훨씬 큰 경우의 수임을 알 수 있다. 즉, 2^n은 일어날 확률이 매우 적기 때문에 quick sort의 대표 시간복잡도는 O(n^2)이 아닌 O(nlogn)이 되는 것이다.
6. Selection Problem
n개의 데이터에 대해서 정렬된 결과로, 특정 key 값을 찾는다고 가정해보자. 만약, n개 중 최솟값을 찾는 다면 n-1번의 키값비교만 하면 되기 때문에 linear time이 걸릴 것이고, 최댓값을 찾는 것도 마찬가지 일 것이다. 그렇지만, 2번째로 작은 수를 찾는 것은 얼마나 걸릴까? 2번째로 작은수와 최솟값을 동시에 구하거나, 3번째로 작은 수와 2번째로 작은 수를 동시에 구하거나 언제나 linear time이 걸릴 것이다.
그렇지만 중간값을 찾는 것은 어떨까? 꼭 중간값이 아니더라도,10만개의 data 중에서 상위 10%에 있는 값을 찾는 거라면? 아마 정렬을 이용하지 않고서는 찾기 힘들 것이다. 그렇기 때문에 적어도 O(nlogn)의 시간이 걸릴 것이다. 그렇지만, 이 방식을 linear time으로 구할 수 있는 방법이 있다. 차례대로 알아보자.
-QuickSelect와 Rselet
먼저 알아볼 방법은 QuickSelect와 Rselect이다. QuickSelect는 Quick sort와 비슷하게 parition을 이용하는 것이다. 다음 수도 코드를 알아보자
QuickSelect(A[1..n],k)
1. Partition A[1..n] (A[j]을 pivot으로 이용해서)
==> A[1..j-1]A[j]A[j+1..n]
2. If j=k
return A[j](pivot)
else if k<j
QuickSelect(A[1..j-1],k)
else
QuickSelect(A[j+1..n],k-j)
이 코드를 보면, Quick sort와 비슷하게 다음 2가지 상황이 발생할 수 있다.

왼쪽은 최악의 경우로, 시간 복잡도가 O(n^2)될 수 있고, 오른쪽은 일반적인 경우로, 시간 복잡도가 O(n)이 되는 것을 볼 수 있다. Quick sort에서 cf.쪽과 같이 최악의 경우가 적게 일어나므로 대표 시간 복잡도는 O(n)이 됨을 짐작할 수 있다.
이 QuickSelection 방법도 좋지만, 항상 pivot을 첫 번째 값으로만 정해야 할까? 랜덤하게 pivot을 정하면 운 좋게 한 번에 원하는 값을 찾을 수 있지 않을까라는 생각에 나타난 것이 RSelect 방법이다. RSelect는 QuickSelect에서 크게 바뀐 것은 없다. 다음 수도 코드를 한 번 살펴보자.
RSelect(A[1..n],k)
1. Choose a random pivot from A[1..n]
2. Partition using the pivot
==>A[1..j-1][j][j+1..n]
3. If j=k,
return A[j] (pivot)
else if k<j
RSelect(A[1..j-1],k)
else
RSelect(A[j+1],k-j)
RSelcet는 random pivot으로 partition만 하면 된다. 이는 어짜피 Quick Select와 바뀐 것이 없기 때문에, 시간 복잡도는 QuickSelect와 동일하다.
-DSelect
이번에는 random pivot을 택하기 보다는 median of median을 이용해서 값을 찾는 과정인 DSelect를 살펴보자. 이 DSelct는 위의 QuickSelect/RSelect와 달리 항상 시간복잡도가 O(n)이 된다. 이를 이해하기 위해서 먼저 다음 수도 코드를 먼저 살펴보자.
DSelect(A[1..n],k)
1. Find medians of subarrays A[5m+1..5m+5] of size 5, m=0...,n/5;
put them into array M[0..n/5]
2. mom = DSelect(M[0..n/5], n/10) //recursive call; meian of median
3. Partition A[1..n] using mom as a pivot
==>A[1..j-1][j][j+1..n]
4. If j=k
return A[j]
else if k<j
DSelect(A[1..j-1],k)
else
DSelect(A[j+1..n],k-j)
위 코드에서는 먼저 A의 원소를 5개씩 묶어서 subarray들을 만들고 각 subarray들의 중간값을 배열 M[0..n/5]에 넣는다. 그 중 다시 DSelect로 median 값을 찾는 방식이다. 그 mom으로 이제 QuickSelect, Rselect와 비슷하게 partition을 진행하고 값을 찾는 것이다.
이 때 j, 즉 pivot값은 n개의 키값중에 어디쯤 위치할지 유추할 수 있게 된다. 결론부터 말하자면 j 값은 상위 30%~70%에 위치하게 된다. 그 이유는 다음 그림을 살펴보면 이해할 수 있다.
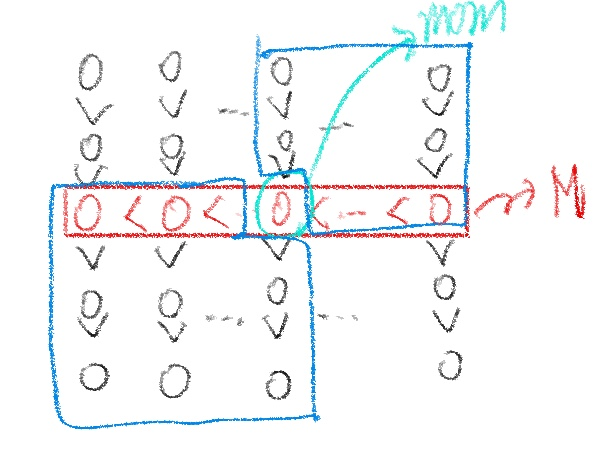
이 그림을 보면 빨간색은 M 배열에 들어간 중간값들이고, 그 중의 또 가운데 값이 mom이 된다. 그 전에, 우리는 A를 5개의 원소로 구성되는 subarray로 쪼갰다. 이를 크기순으로 다시 배열하면, 위 그림과 같이 나온다.
이 때, mom 값보다 확실히 작은 값들과, 확실히 큰 값은 파란색으로 표시한 영역이 된다. 이는 일반적으로 각각 전체 원소 중 30%를 차지하게 됨을 알 수 있다. 그 이유는 mom값보다 작은 부분은 전체 n개의 원소 중 mom을 기준으로 1/2n 부분 중에서도 3/5를 차지하므로 3/10n개 즉, 30%임을 알 수 있고, 다른 파란색 부분도 마찬가지이다. 이를 통해 위에서 서술한 j값 즉 mom값은 상위 30%에서 70% 사이에 존재함을 알 수 있다.
그럼 이 DSelect의 시간 복잡도를 알아보자. DSelect의 실행 시간을 T(n)이라고 하면 T(n)은 다음과 같이 표현할 수 있다.
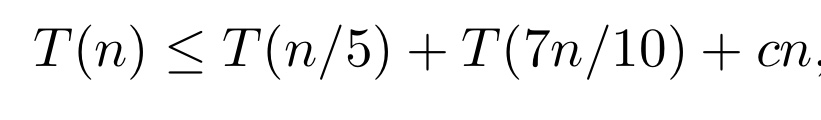
그 이유는 일단, mom을 고르는 시간은 T(n/5), 4에서 mom 기준으로 상위 30%나 하위 30%를 제외하고 다시 재귀적으로 값을 찾는 실행시간이다. Cn은 정렬하는 시간이다.
mom을 고르는 시간이 T(n/5)인 이유는 일단, n개의 배열에서 5개의 subarray로 만들고, 그 뒤에 각 중앙값들을 구해서 배열 M에 넣어야 된다. 이 때, 각 배열의 중앙값들을 구하는 시간은 크기가 5로 정해져 있으므로 상수 O(1)의 시간복잡도를 가진다. subarray 수가 (n/5)이므로, subarray들의 모든 중앙값을 구하는 시간 복잡도는 O(n)이다. 그 뒤, M의 배열의 원소 수는 n/5가 되는데, 이 때 또 중앙값을 찾는 시간 복잡도는 O(n/5)이기 때문에 실행시간이 T(n/5)가 된다.
이 때, quickSelect에서 언급했듯이, 1/5+7/10=9/10<1일 경우에는 시간 복잡도가 O(n)임을 알 수 있다. 이렇기 때문에 DSelect의 시간복잡도는 O(n)으로 나타낼 수 있다는 것이다.
cf. 만약 n/3+2n/3으로 하는 경우, 즉 3개로 쪼개 mom을 찾는 경우에는 어떻게 될까? 이 경우 Quick sort에서 봤듯이 α,1- α 로 하는 경우와 동일하기 때문에 시간 복잡도가 O(nlogn)이 된다.
7. 정리
이번 정리글에서는 Divide & Conquer라는 알고리즘 기법에 대해 살펴보았다.
Divide & Conquer 방식에는 다양한 응용이 있으며, 각 방법마다 시간 복잡도가 왜 그렇게 되는지, 그리고 어떤 방식이 더 개선된 방법인지 정확히 이해하고 기억해 두는 것이 중요하다.
다음 글에서는 Divide & Conquer보다 더 나아간 방식인 Dynamic Programming 알고리즘에 대해 정리할 예정이다.
'학교공부 > [알고리즘 분석]' 카테고리의 다른 글
| [알고리즘 분석] - Graph Algorithm_Strongly Connected Components (0) | 2025.06.06 |
|---|---|
| [알고리즘 분석] - Graph Algorithm_BFS, DFS (1) | 2025.06.06 |
| [알고리즘 분석] - huffman code (0) | 2025.05.23 |
| [알고리즘 분석] - 피보나치 (2) | 2025.04.17 |
| [알고리즘 분석] - 수도코드 및 시간 복잡도 (0) | 2025.04.16 |



