이전 글에서는 Control plane에 대해서 정리하며, 라우팅 알고리즘의 분류까지 정리해 보았다. 이번 글에서는 라우팅 알고리즘 중, 분류에서는 global한 알고리즘에 해당하는 link-state 방법에 대해서 정리해 볼 예정이다.
1. Dijkstra's link-state routing algorithm
그럼 link-state라는 방법은 어떻게 진행되는지 한 번 살펴보자.
link-state는 알고리즘 분석글에서 정리했던 Dijkstra's algorithm 방식을 채택했다. Dijkstra's algorithm 방식에 대해 더 자세한 정리는 여기를 클릭하면 된다.
간단히 다익스트라 알고리즘에 대해서 설명하면, 주어진 weighted 그라프에서 하나의 노드로부터 모든 다른 노드까지의 최단 경로를 찾는 알고리즘 방식이다.
Dijkstra 알고리즘을 활용한 link-state 방식은, 각 라우터가 네트워크 상의 모든 다른 라우터까지의 최단 경로를 계산하는 방식이며, 이를 Dijkstra link-state routing algorithm이라고 부른다.
그럼 이 다익스트라를 이용한 link-state 알고리즘을 더 자세히 알아보자.
코드를 알아보기 전에 짚고 넘어가야 될 점은 다음과 같다.
- link-state : centralized로 분류된 라우 알고리즘으로, 각 링크의 비용 정보를 모든 라우터가 공유하고 있어야 한다. 이 정보는 링크 상태 광고를 통해 네트워크 전체에 broadcast되며, 결과적으로 모든 라우터는 동일한 네트워크 토폴로지 정보를 갖게 된다.
- C(x,y) : 노드 x로부터 y까지의 direct(직접 연결된) link의 cost
- D(v) : source로부터 destination v까지 현재 least-cost path의 추정치
- p(v): source부터 v까지의 최단 경로 상에서 v 직전에 위치한 노드
- N' : 최소 비용 경로가 확정된 노드들의 집합
2. Dijkstra's link-state routing algorithm code
Initailization:
N' = {u}
for all nodes v
if v adjacent to u
then D(V) = C(u,v)
else D(v) = ∞
Loop
find w not in N' such that D(w) is a minimum
add w to N'
update D(v) for all v adjacent to w and not in N':
D(v) = min(D(v),D(w)+C(w,v))
until all nodes in N'
위 코드는, 알고리즘 분석의 Dijkstra's shortest-path algorithm 글 코드와 비슷하기 때문에, 코드에 대한 설명은 해당 글을 참고하자.
해당 코드를 이용해 다음 주어진 상황을 link-state 알고리즘을 해결해보자. 이때 시작점은 u라고 가정한다.
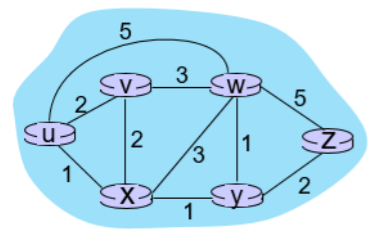
| Step | N' | D(v),p(v) | D(w),p(w) | D(x),p(x) | D(y),p(y) | D(z),p(z) |
| 0 | u | 2, u | 5, u | 1, u | ∞ | ∞ |
| 1 | ux | 2, u | 4, x | 2, x | ∞ | |
| 2 | uxy | 2, u | 3, y | 4, y | ||
| 3 | uxyv | 3, y | 4, y | |||
| 4 | uxyw | 4, y | ||||
| 5 | uxywz |
각 step 별로 설명하면,
- 0 : 모든 노드를 다 초기화 한 뒤, u를 pop한 상태로, u와 direct하게 연결된 노드들의 거리를 계산해서 업데이트하고, 이전 노드의 값을 가리키는 p를 u로 설정한다. y,z는 값을 모르기 때문에 ∞로 초기화한다.
- 1 : D 값이 가장 작은 x를 선택하여 N′에 추가하고, x와 인접한 노드들의 D 값을 업데이트한다. 예를 들어, u → x → w 경로의 비용이 u → w보다 더 짧다면, D(w)와 p(w)를 새롭게 갱신한다.
- 모든 노드가 N'에 포함될 때까지 위 과정들을 반복한다.
위의 알고리즘 적용 결과로 다음과 같은 least-cost-path tree를 얻을 수 있다.
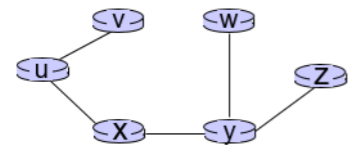
위의 least-cost-path tree를 바탕으로, forwarding table을 작성하게 되는데, 라우터 u에서는 다음과 같은 forwarding table이 나타난다.
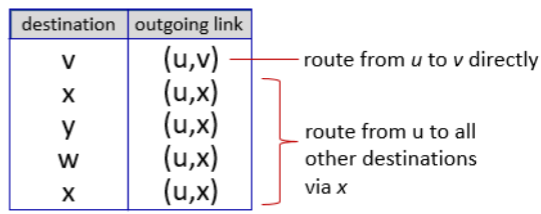
다익스트라 link-state 알고리즘을 이용하면, 시간복잡도는 O((n+m)logn)이다. 더 자세한 것은 알고리즘 분석-다익스트라 글을 참고하자.
대신, 다익스트라 link-state 알고리즘 방식의 message complexity에 대해서 더 자세히 다뤄볼 것이다.
라우팅에서는 각 라우터가 자신의 링크 상태 정보를 네트워크 전체에 broadcast해야 하므로, message complexity는 링크의 수에 따라 결정된다. 이론적으로는 완전 연결된 네트워크의 경우 n(n−1)/2개의 링크가 존재할 수 있지만, 실제 네트워크에서는 이보다 훨씬 적은 수의 링크만 존재한다. 예를 들어, link가 여러개 연결되어 있다고 하더라도, 실제 쓰는 link는 cost가 제일 적은 link일 것이기 때문에 실제 링크의 수는 n^2에 수렴하지 않고 n에 가깝다.
따라서 일반적으로 n개의 노드가 적절하게 연결되어 있다고 가정하면, 각 노드는 자신의 인접 링크 정보를 broadcast 해야 하므로 전체 message complexity는O(n^2)이다.
3. Dijkstra's algorithm : Oscillations(경로 진동 현상)
Dijkstra 알고리즘 기반의 Link-State 라우팅에서는, 네트워크 혼잡도나 링크 비용이 실시간으로 변할 경우 경로가 계속해서 바뀌는 진동 현상(Oscillation)이 발생할 수 있다.
위의 예시들은, 다익스트라 알고리즘을 통해 라우팅을 한 번만 계산하는 과정을 보였는데, 사실 link의 cost는 혼잡도에 따라 실시간으로 달라지며, routing algorithm도 이를 반영해 실시간으로 least-cost-path를 갱신해야 된다. 이를 위한 예시를 한 번 살펴보자.

위 그림은, 초기에, routing algorithm을 통해 결정한 경로이다. 이때, e<1이고, 0은 해당 link를 이용하지 못하는 상태라고 가정해보고, 설명하면,
- c에서 a로 가는 경로는 c-b-a(c>b : e, b>a : 1, 총 :1+e)로 결정되었고, d에서 a로 가는 경로는 d-a(d>a : 1)이다.
이후, 혼잡도가 증가함에 따라 link cost도 갱신되기 때문에, routing algorithm을 다시 실행시켜야 한다. 다음 그림을 통해 상황을 살펴보면,

- c에서 b, b에서 a로 가는 경로가 0이 되었기 때문에, 초기의 c-b-a 경로를 택할 수 없다.
- 이때, b에서 a로 가는 경로(c에서 a로 가는 경로도 이에 포함됨)가 갱신된다.
- 총 2+e로 갱신이되며, 초기값과 반대 방향으로 경로가 갱신이 된다.
이때, 다시 또, b에서 c로 가는 길이 0이 되고, c에서 b로, b에서 a로 가는 경로가 다시 열리게 되면 초기값과 비슷한 경로로 돌아오게 된다.
즉, 이런 상황은 흔히 발생할 수 있는데, 처음에는 시계방향으로 경로를 구성했다가 해당 경로에 트래픽이 몰리면 반시계방향으로 경로를 재계산하고, 다시 그쪽에 트래픽이 몰리면 또 시계방향으로 돌아오는 식으로 경로가 반복적으로 바뀌는 진동 현상(oscillation)이 발생한다.
이러한 경로 진동은 바람직한 라우팅 방식이라고 볼 수 없으며, 이를 완화하기 위한 대안이 필요하다. 각 경로를 균등하게 나눠 쓰는 방식, 또는 Distance Vector 방식이 이를 해결할 수 있다.
+)Distance vector 방식은 다음 글에서 정리할 예정이다.
'학교공부 > [컴퓨터 네트워크]' 카테고리의 다른 글
| [컴퓨터 네트워크] - Network Layer_OSPF (1) | 2025.06.08 |
|---|---|
| [컴퓨터 네트워크] - Netowrk Layer_Distance vector (1) | 2025.06.07 |
| [컴퓨터 네트워크] - Network Layer_Control Plane (0) | 2025.06.06 |
| [컴퓨터 네트워크] - Network Layer_Middleboxes (0) | 2025.06.06 |
| [컴퓨터 네트워크] - Network Layer_Generalized Forwarding (0) | 2025.06.06 |



