이전 정리글에서는 network layer의 control plane에 해당하는 routing 알고리즘 방법 중, 다익스트라를 활용한 방식인 link- state 방법에 대해서 정리해 보았다.
마지막 부분에, link-state 방식의 단점을 설명하며 그 보완책으로 Distance vector에 대해서 언급했었는데, 이번 글에서는 라우팅 알고리즘 방법 중 하나인 Distance Vector에 대해서 정리해보려고 한다.
1. Bellman-Ford(BF) Equation
Distance Vector 방법에 대해서 정리하기 전에, Distance vector가 base로 두는 Bellman-Ford 방정식에 대해서 알아보려고 한다. 이 방정식은 다음과 같이 정의된다.

즉, x에서 y까지 경로에 대해 least-cost-path의 cost는 위의 식처럼 표시한다는 것이다. 각 항의 의미는 다음과 같다.
- minv : x의 이웃(직접 연결되어 있는) 모든 v에 대한 최솟값
- c(x,v) : x에서 v까지의 direct cost
- Dv(y) : v에서 y까지의 least-cost-path cost의 추정치
위 식을 보면, 재귀적인 형태를 띄고 있다는 것을 알 수 있다.
위 방정식을 적용한 예시를 한 번 살펴보자.

시작점은 u라고 가정하고, u의 이웃 노드인 x,v,w,이며, x,v,w는 목적지 z까지의 값을 안다고 가정하자. 이 그림에 대해 Bellman-Ford 방정식을 통해 Du(z)를 구하면 다음과 같이 나타낼 수 있다.

즉, u에서 z까지의 거리의 최솟값은 목적지까지 경로를 알고 있는 u의 이웃 노드들 중 최솟값을 구한 것이다. 즉, 이를 그림으로 나타내면 다음과 같이 표현할 수 있다.
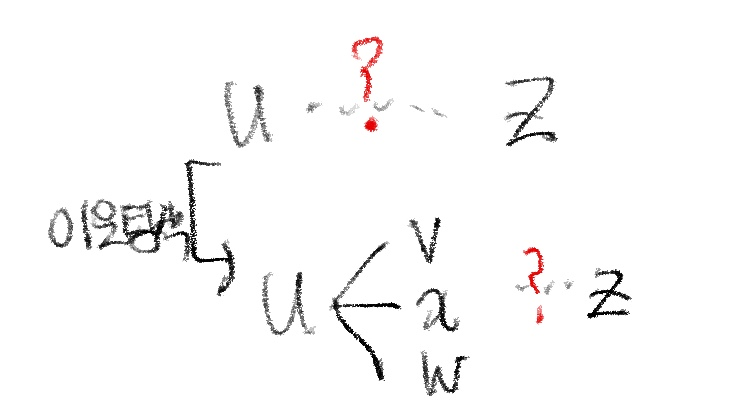
즉, u에서 z까지의 경로를 구할 때 전체 경로를 모르므로, u는 이웃 노드들을 탐색하게 된다. 그리고 각각의 link cost를 계산한 뒤, 그 이웃 노드로부터 z까지의 경로도 다시 고려한다. 이때 이웃 노드들이 z까지의 경로를 알고 있다면 그 값을 활용하고, 직접 연결되어 있다면 그 값을 그대로 더해서 u에서 z까지의 최단 경로를 구하게 되는 것이다.
2. Distance Vector Algorithm
이제 본격적으로 distance vector algorithm에 대해서 정리해 보려고 한다.
Distance Vector Algorithm의 주요 아이디어는 다음과 같다.
- B-F(Bellman-Ford) 방정식을 이용한 최단경로 cost 갱신
- distance vector값이 갱신될 때마다, 각 노드는 그 노드가 알고있는 distance vector 값을 이웃노드에게 알린다.
- 자연스레, Dx(y)값은 실제 최단 경로 cost 값으로 수렴한다.
위 아이디어를 통해, link-state 방식과는 확연히 다른 방식이라는 것을 알 수 있다. 특히 두번째 특징을 살펴보면, 모든 노드에게 계산 결과를 broadcast하는 global한 link-state 방식과 달리, 이웃 노드에게만 정보 공유를 한다는 점에서 로컬 기반 방식임을 알 수 있다.
그럼 위 idea를 적용한 distance vector 방법에서 각 노드는 무슨 일을 할까?
- 이웃으로부터 메세지가 오거나 local link cost가 바뀔 때까지 기다린다.
- 이웃으로부터 전달받은 DV를 통해 자신의 DV값을 다시 계산한다.
- DV값이 바뀌면, 이웃에게 갱신된 값을 알린다.
위의 1,2,3 방식이 계속 반복하며 알고리즘이 동작하게 된다.
Distanc Vector 방식은 다음과 같은 특징을 가지고 있다.
- iterative, asynchronous:
- iteration은 local link cost가 바뀌거나 이웃으로부터 DV update message를 받았을 때만 일어난다.
- 따라서, 실시간으로 변화하는 vector 값에 대해 같은 시점에 같은 값을 가질 수 없다.
- distributed, self-stopping:
- 각 노드는 오로지 DV값이 변화했을 때만 이웃 노드에게 알린다
- 즉, 값이 변경되면 필요할 경우에만 이웃에게 알리고, 그 외에 notification이 없으면, 스스로 멈춘다.
이러한 특징들로 인해 Distance Vector 방식은 로컬 환경에서 구현이 간단하며, 분산 컴퓨팅 환경에서도 자연스럽게 작동할 수 있다.
이제 Distance vector의 예시를 한 번 살펴보자.
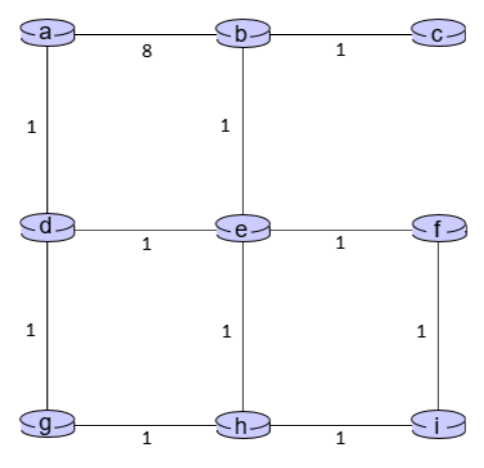
위 그림과 같이 a~i까지의 라우터와 연결된 각 link의 cost값이 주어져 있다고 가정해보자. 이때, b를 기준으로 예시를 들어보려고 한다.
b는 DV를 계산하는데, 다음과 같이 계산된다.

즉, 초기에는 direct 하게 연결된 a,c,e값의 DV밖에 모른다. 그렇지만 이때, a,c,e로 부터 DV값을 공유 받게 되면,



b는 다시 DV 값을 다음과 같이 계산한다.
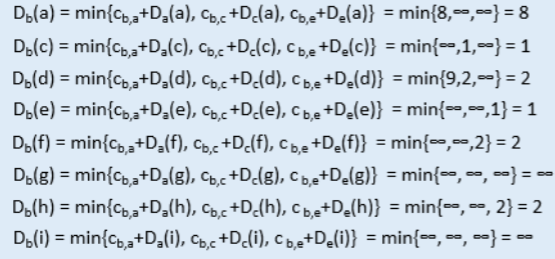
즉, a,c,e를 통해 갈 수 있는 노드들이 생기거나, 최단 경로 값이 갱신되면 b의 DV는 해당 결과를 반영한다. 따라서 위 계산을 진행한 결과, b는 다음과 같은 DV값들을 가지게 된다.

b의 DV 값이 변경되었기 때문에, b는 갱신된 DV 값을 이웃 노드인 c와 e에게 전달한다. 이후, a, c, e는 전달받은 정보를 바탕으로 각각 자신의 DV 값을 다시 계산하며, 이 과정을 반복하여 전체 네트워크의 DV가 점진적으로 수렴하게 된다.
3. Distance vector : state information diffusion
이 distance vector 방식은, diffusion이라는 특징을 가지고 있는데, DV 계산결과가 점차 확산한다는 것이다. 다음 그림을 확인해보자.

위의 예시와 같은 그라프의 모양이지만, 이번에는 라우터 C를 기준으로 시간(t)이 지남에 따라 C의 DV값이 어디까지 영향을 미치는 지 알아보려고 한다.
| 시간 | 상태 |
| t = 0 | c는 본인의 DV을 계산한다. |
| t = 1 | b에게 본인의 DV를 공유하고, 마찬가지로 b의 정보를 받는다. 즉, 1 hop 차이인 노드와 DV를 공유한다. |
| t = 2 | c의 t=0일 때의 DV 값이 1 hop차이인 노드들에게 반영됐고, 이제 c 기준으로 2 hop차이인 노드들에게 이 정보가 공유된다. |
| t = 3 | c의 t=0일 때 DV 값이 2 hop 차이인 노드들에게 반영됐고, 이제는 3 hop차이인 노드들에게 이 정보가 공유된다. |
| t = 4 | 마지막으로, t=0일 때 DV 값이 3 hop차이인 노드들에게 반영되고, 4 hop차이인 노드들에게 공유된다. |
즉, c의 t=0일 때의 DV 값이 hop 거리에 따라 점차 확산되는 모습으로 보이기 때문에, Distance vector는 diffusion하다는 특징을 가지게 된다.
4. Distance vector : link cost changes
앞서 계속 언급했듯, 네트워크 상황에서 link cost는 계속 변화한다. 이러한 특성 때문에, link-state 방식에서는 경로의 주기적인 재계산이 빈번하게 일어나 오버헤드 증가 등 바람직하지 않은 상황이 발생할 수 있다. 그러면, Distance vector는 어떨까?
Distance vector는 "good news travels fast, bad news travels slow"라는 특징을 가지고 있다. 즉, 좋은 소식(경로 개선)은 빠르게 전파되고, 나쁜 소식(경로 악화)은 느리게 전파되는 특징을 가지고 있다.
먼저, link-cost가 줄어든 good news 상황에 대해 정리해 보려고 한다. 다음 예시를 한 번 살펴보자.
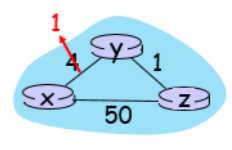
위 그림에 대해서 설명하면,
- 노드 x,y,z가 존재하고 초기 link cost는 x-y : 1, x-z : 50, y-z : 1이다.
- 이때, x-y의 link cost가 4에서 1로 바뀌었다.
link cost의 변화가 생긴다면, 다음과 같은 상황이 발생한다.
- node는 본인과 연결된 link의 cost 변화를 detect한다.
- routing 정보를 update하고, DV의 값을 다시 계산한다.
- DV값이 변한다면, 이웃에게 알린다.
이를 위 그림의 시간에 따른 변화로 정리하면 다음과 같다.
| 시간 | 상태 |
| t0 | y가 link-cost가 변화한 것을 detect하고, DV를 업데이트한 뒤, 이웃에게 알린다. |
| t1 | z가 y로부터 업데이트 상황을 보고 받고, DV를 업데이트한다. 특히, x까지의 최단경로를 5에서 2로 업데이트 하고, y에게 알린다. |
| t2 | y는 z로부터 업데이트 상황을 보고 받고, DV를 업데이트 한다. y는 기존에 기록한 최단 경로 중 변한 값이 없어, z로 추가 메세지를 보내지 않는다. |
그럼 다음 그림과 같이 link cost가 증가한 bad news 상황에 대해서 정리해 보겠다.

즉, 그림은 x-y link-cost가 4에서 60으로 크게 증가한 경우이다.
마찬가지로, node는 link cost 변화를 감지하는데, 다음 순서로 동작한다.
- y는 x와 direct하게 연결된 link-cost가 60으로 늘어난 것을 확인하고, y은 DV값을 업데이트하려고 한다.
- 이때, Dy(x) = 60으로 설정하지 않고 주변 DV값들을 다 참조하는데, z에서 Dz(x)=5인것을 확인하고, B-F 방정식을 이용해 다음 계산을 진행한다.
- Dy(x) = min{60, c(y,z) + Dz(x)} = min{60, 1+5} = 6
- 따라서 z를 통해 x로 가면, 6으로 갈 수 있다고 생각하며, Dy(x)=6으로 업데이트하고, 이웃들에게 알린다.
- z는 y로부터 업데이트된 DV를 받고, B-F 방정식을 이용해 다음 계산을 진행한다.
- Dz(x) = min{50, c(z,y) + Dy(x)} = min{50, 1+6} = 7
- 따라서 y를 통해 x로 가면, 7로 갈 수 있다고 판단하여 Dz(x)=7로 업데이트하고, 이웃들에게 알린다.
- 위 상황을 Dz(x) = 51이 될 때까지 반복하게 된다. Dz(x) =51이 되는 순간, Dz(x)의 최솟값이 direct link-cost인 50으로 바뀌기 때문이다. 즉, ping-pong 상황이 발생하게 된다.
이처럼, link cost가 증가한 bad news 상황에서는 Distance Vector가 잘못된 정보를 기반으로 DV를 점차 증가시키는 반복 과정에 빠지게 되며, 결국 이것이 바로 count-to-infinity problem이다.
당연히 위를 해결하기 위한 방법의 알고리즘도 등장했는데, 바로 Poison Reverse Algorithm이다.
이 알고리즘은, 위에서 언급한 ping-pong 과정을 막기 위한 방법이다. 이 알고리즘을 위의 상황에 적용하면 다음 순서로 동작한다.
- y는 초기에 이웃들에게 Dy(x) = infinity로 알린다.
- 그리고 위 그림과 같이, y-x의 link cost가 올라가면, 그 올라간 값을 전달한다. 그럼 Dy(x) = 50으로 이웃들에게 알리는 것이다.
- 이렇게 되면, z 입장에서는 Dz(x)가 원래 50에, 전달받은 값은 60이기 때문에 y를 거쳐 갈 필요가 없다고 판단하여 DV 값을 업데이트 하지 않는다.
이 알고리즘을 이용하면, ping-pong 문제를 해결할 수 있을 것 같이 보이지만, 다음 그림과 같은 문제점이 존재한다.
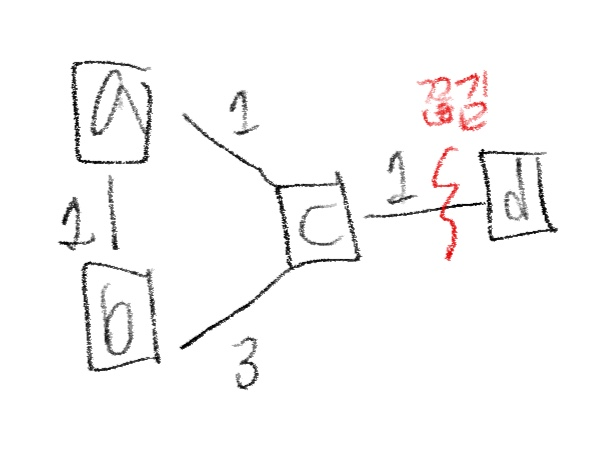
위 그림을 살펴보면, link cost는 각각 a-b:1, a-c:1, b-c:3, c-d:1이다. 그리고 posion reverse algorithm을 이용한다는 가정하에 초기값은 Db(d)=Da(d)= ∞이다. 그리고, 시간이 조금 지나고 안정된 상태가 되면, 다음과 같이 값이 갱신된다.
- Db(d) = 3, Da(d) = 2
- a에서 d로가는 경로 : a-c-d
- b에서 d로 가는 경로 : b-a-c-d
이때, 위 그림처럼, c-d 사이의 link가 끊긴 상황이라고 가정해보자. 이 상황에 다음과 같이 진행된다.
- c가 d와의 연결 끊김 감지하고 Dc(d) = ∞로 설정 즉, Poison Reverse로 인해 a, b에게 c를 거치는 방식으로 더 이상 d로 갈 수 없다고 알린다.
- 이때 c는 새로운 경로를 찾으려고 시도한다.
- 이때, 쓰이지 않고 있던 Db(c) = 3을 보고, c는 b를 통해 d로 갈 수 있을거라 착각하게 된다. 따라서, B-R 방정식을 이용해
- Dc(d) = min{∞, c(c,b) + Db(d)} = min{ ∞,3+3} =6으로 업데이트한 후, a,b에게 알린다.
- 해당 값을 전달 받은 a,b도 이제, d로 갈 수 있는 새로운 경로가 생겼다고 착각하여 DV값을 다시 업데이트 한다.
- 이렇게 ping-pong이 계속되고 무한루프가 시작된다.
Posion Reverse Algorithm은 위와 같은 상황에서는 count-to-infinity 문제를 해결할 수 없다.
5. Link-State vs. Distance Vector
해커들 입장에서, 수많은 트래픽이 거쳐가는 라우터를 해킹하는 것은 매우 매력적이다. 만약 해커나 악성 사용자가 라우터의 라우팅 정보를 고의로 조작하거나, 라우터 자체의 소프트웨어 결함으로 인해 잘못된 정보를 광고하게 된다면,
네트워크 전체에 치명적인 영향을 줄 수 있다.
- Link State
- 각 라우터는 전체 네트워크의 토폴로지 정보를 수집하고, 이를 기반으로 자체적으로 라우팅 테이블을 계산한다.
- 하지만, 만약 특정 라우터가 고의로 혹은 실수로 부정확한 link cost를 광고한다면, 해당 정보가 다른 모든 라우터에 전파되어 전역적인 혼란을 야기할 수 있다.
- Distance Vector
- 각 라우터는 자신이 계산한 경로 정보를 이웃에게만 전파한다.
- 문제는, 이웃 노드의 정보에 전적으로 의존한다는 점이다. 이웃이 고의로 부정확한 정보를 전파하거나, 계산 오류를 발생시키면 그것이 전파되며 네트워크 전체에 점차 확산될 수 있다.
따라서 위 특징들을 보면, Link-State 방식은 각 라우터가 독립적으로 계산을 수행하므로 이웃 노드의 정보에 의존해 동작하는 Distance Vector 방식이 구조적으로 더 취약하다고 볼 수 있다.
그렇지만, link state 방법도, 모든 라우터의 link 상태를 저장하고 유지해야 되기 때문에 메모리와 계산 비용이 더 많이 들 수도 있다.
결국, Link-State와 Distance Vector 간에는 보안성과 성능 사이의 trade-off가 존재한다. 따라서 실제 네트워크에서는 한 가지 방식만 쓰지 않고, 두 가지 방식의 특성과 장단점을 고려하여 선택하거나, 후에 정리할 라우팅 프로토콜(OSPF 등)을 활용한다.
'학교공부 > [컴퓨터 네트워크]' 카테고리의 다른 글
| [컴퓨터 네트워크] - Netowrk Layer_BGP (4) | 2025.06.12 |
|---|---|
| [컴퓨터 네트워크] - Network Layer_OSPF (1) | 2025.06.08 |
| [컴퓨터 네트워크] - Network Layer_link-state (0) | 2025.06.07 |
| [컴퓨터 네트워크] - Network Layer_Control Plane (0) | 2025.06.06 |
| [컴퓨터 네트워크] - Network Layer_Middleboxes (0) | 2025.06.06 |



