지난 글에서는 CNN의 각 Layer와 그 Layer가 하는 일들에 대해서 알아보았다. 이번에는 Activation Function들에 대해서 알아보려고 한다.
1. Activation Functions
그럼 과연 이 Activation Functions는 무엇일까? 이전에, CNN은 선형함수와 비선형함수의 결합으로 복잡한 함수를 표현할 수 있다고 정리했다.
그런데, 만약 모든 Layer가 선형함수로만 구성되어 있다면, 아무리 많이 Layer를 쌓는다해도 결국 하나의 선형함수로 표현되게 된다. 이렇게 되면, CNN이 학습할 수 있는 표현력에 한계가 생긴다.
이 문제를 해결하기 위해 각 Layer의 출력에 비선형 함수를 결합해준다. 이 비선형 함수를 바로 Activation Function이라 하는 것이다.
이 함수는 입력값이 특정 임계값을 넘거나, 혹은 특정 형태로 변형되도록 하게 해 모델이 비선형적이고 복잡한 패턴을 학습할 수 있게 도와준다. 따라서 최종적으로 f(x)는 다음과 같이 표현된다.

2. Activation Functions의 특징
그럼 이 Activation Functions는 무슨 역할을 하며 어떤 특징을 지닐까?
먼저, Activation Functions의 특징은 다음과 같다.
- 실제 학습대상은 아니다. 즉, 함수 형태 자체가 고정되어 있고, 사전에 선택해야 한다.
- 최대한 단순하게 나타내야 한다. 보통 미분이 간단하고 빠른 단순한 형태의 함수를 사용한다.
- Neural Network에서 핵심 요소이다.
이 Acitvation Functions는 앞서 언급했듯, 입력 값이 일정 수준(Threshold) 이상이어야 출력이 나온다. 즉, 뉴런처럼 일정 이상의 자극이 있어야 신호 전다를 하는 것처럼, 일정 값(Threshold)을 넘어서야 계산이 진행되고 출력이 나오게 된다.
보통, 역치 이상이라함은 다음과 같은 그림으로 표현된다.

이렇게 나타낸 함수를 Step Function이라고 한다. 하지만, 이 함수는 미분을 진행할 수 없게된다. 미분을 하지 못하게 되면, Back Propagation을 적용할 수 없게 되는데, 이럴 때는 미분 불가능한 지점을 미분 가능하게 만들면 된다. 이 아이디어는 다음과 같이 표현된다.

이런 방식으로 나타낼 수 있으면, 미분 가능해지고, back propagation을 적용할 수 있다.
이런 방식으로 나타낸 함수들이 바로 Activation Functions이다. 대표적인 예시들은 다음과 같다.
- Sigmoid
- tanh
- ReLU
- Leaky ReLU
- Maxout
- ELU
이중, Sigmoid와 ReLU, LeakyReLU와 ELU에 대해서 살펴보자.
- Sigmoid
Sigmoid는 step function과 매우 유사하게 생겼지만 미분 가능하다는 특징이 있다. Sigmoid는 다음과 같이 표현된다. 입력이 작으면 0, 크면 1에 가까워진다.

그러나, 이 Sigmoid에는 치명적인 단점이 존재한다. 입력값이 너무 크거나 작을 때, 미분값이 0에 가까워진다는 것이다. 즉, backpropagation을 진행할 때, Gradient가 사라지는 현상, Gradient Vanishing 문제가 발생한다. 이 때문에 NN의 Layer가 많아질수록, 학습이 제대로 진행되지 못하게 된다.
따라서, Sigmoid함수는 Step function과 가장 유사하지만, 최근에는 많이 쓰이지 않는 함수이다.
- ReLU
다음으로 알아볼 Activaion Function은 ReLU이다. ReLU는 앞선 Sigmoid의 Gradient Vanishing 문제를 개선하기 위해 나온 함수이다. ReLU는 전달받은 값이 0보다 클 때 미분값이 0이 되는 문제를 해결했다. 어떻게 해결했는지 보면, 다음 식과 그래프를 보면 이해할 수 있다.

즉, 0과의 비교를 통해 최댓값을 적용시키는 것인데, x>0인 부분에서는 모든 값들이 f(x) = x로 표현되기 때문에, 미분값이 1로 존재하게 된다. 그렇지만, 여전히 x<0일 때는 Gradient Vanishing 문제가 존재한다.
+) 계산이 단순하고 빠르다는 장점이 있고, Sigmoid보다 학습 수렴 속도가 빠르고 효율적이다.
- Leaky ReLU, ELU
마지막으로 알아볼 Activation Functions는 Leaky ReLU와 ELU이다. 이 함수들은 ReLU의 x<0일 때, Gradient Vanishing 문제를 해결하기 위해 나온 함수다. 각각 어떻게 해결했는지 그래프를 통해 알아보자.

Leaky ReLU에 대해 설명하면 다음과 같다.
- max(ax, x)를 이용한다. (0<a<1)
- 따라서, 0보다 작을 때는 ax를, 0보다 클 때는 x라는 그래프를 선택하게 된다.
- x<0보다 작을 때 미분값이 존재하게 되며, 정상적으로 back propagation을 진행할 수 있게 됐다.
사실, 이 Leaky ReLU를 천천히 다시보면, 0에서 미분 불가능하다는 것을 알 수 있다. 좌미분하고 우미분값이 다르기 때문인데, 이 문제는 그냥 0에서는 미분값을 0이나 a 중 하나를 사용하는 방식으로 처리한다. 이 Leaky ReLU는 이 단점 빼고는 성능이 매우 우수하다.
ELU는 위의 x=0에서 미분 불가능한 문제를 해결한 방식이다.
+) Leaky ReLU는 Transposed Convolution(출력 크기를 확대하고 싶을 때 사용하는 Convolution 방식)에서 사용한다.
3. AlexNet 진행방식에 대한 이해
이제, CNN에 대해서 모든 것을 정리해 보았다. 그럼 이 CNN이 적용되는 대표적인 예시 AlexNet에 대해서 어떻게 이미지를 분류하는지 알아보자.
Alexnet은 총 5개의 Convolutional Layer,3개의 Pool Layer와 FC, Softmax로 구성되어 있다. 추가로, 각 Layer 사이에는 ReLU를 비선형 함수로 이용했다.
- 먼저, 맨 처음으로 Image가 들어온다.
- 첫 번째 Convoluional Layer에서는 edge, 색상 변화, 선 방향 등을 추출하여 feature map으로 만든다.
- 2~3번째 Convolutional Layer에서는 얻은 edge 정보들을 통해 눈, 귀, 타이어 같은 부분 형태를 추출하여 feature map으로 만든다.
- 4~5번째 Convolutional Layer에서는 전체 얼굴, 자동차 실루엣, 동물 실루엣 등 추출하여 feature map으로 만든다.
- FC + Softmax를 통해 확률을 계산한다.
즉, 초기 Convolutional Layer에 있는 필터들은 edge와 같은 단순한 특징을 감지하고, 깊은 Layer로 갈수록 필터들은 detail한 특징까지 잡을 수 있게 되는 것이다.
4. CNN 예시 - GoogLeNet, ResNet
- GoogLeNet
다음으로 알아볼 CNN 예시는 Google에서 만든 GoogLeNet이다. GoogLeNet은 기존 CNN이 Back Propagation을 진행할 때, 너무 많은 Layer가 존재하면, 해당 과정에서 Gradient Vanishing이 나타나는 문제가 있다는 것을 완화시키기 위해 나온 구조이다.
기존의 CNN에서는 Layer가 너무 많아 하위 Layer로 갈수록 미분값이 0에 가까워져 학습이 거의 이루어지지 않는 문제가 발생했다. 이를 해결하기 위해 중간 Layer마다 보조 분류기를 추가해서 Loss값을 계산해 저장해 놓았다.
그리고, 최종 Loss에서 Back Propagation을 진행하다가 Gradient Vanishing 문제가 생길 경우, 보조 Loss 경로를 통해 하위 Layer에서도 학습이 되게 하도록 한 것이다. 이를 통해 기존보다 훨씬 많은 Layer를 쌓고도 안정적으로 학습이 가능해 졌다.
- ResNet
다음은 ResNet이다. ResNet은 다음 그림을 통해 이해하는 것이 좋다.
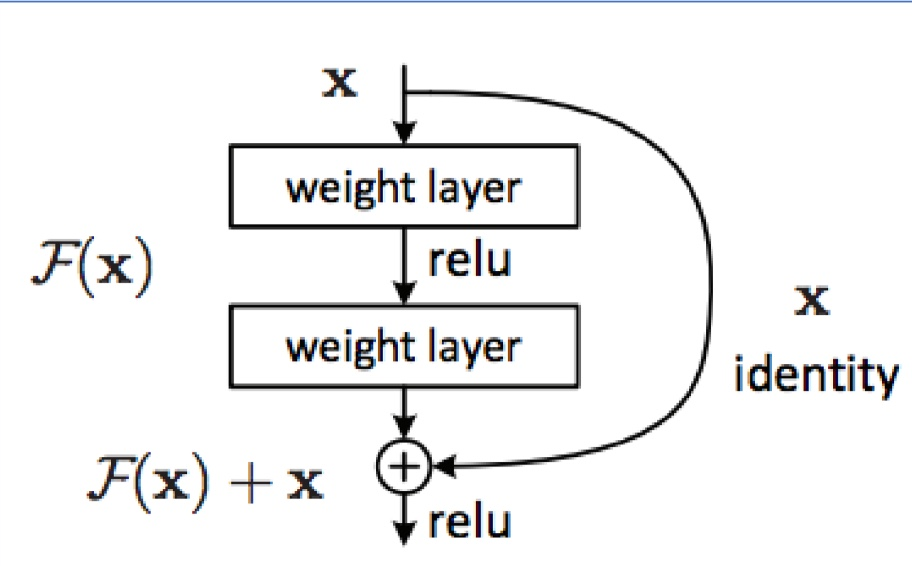
그림에 대해서 설명하면, 입력값 x가 들어왔을 때, 보통 CNN에서는 Layer를 거쳐 계산된 결과 F(x)만 이용해 다음 단계의 비선형 함수를 통과시킨다.
ResNEt에서는 입력값 xfm를 그대로 더한 뒤 비선형 함수를 적용한다. 즉 입력 x를 선형 함수 출력에 직접 더해주는 구조를 사용한다. 이렇게 되면, F(x) + x를 미분하면 F'(x) + 1이 남게 되고, 결국, F'(x)가 사라져도 1이라는 값이 살아남아 back propagation이 계속 진행될 수 있다는 것이다. 즉, 추가적인 back propagation 경로가 생긴 것과 마찬가지이다.
이를 3 Layer를 통해 표현하면 다음과 같다.
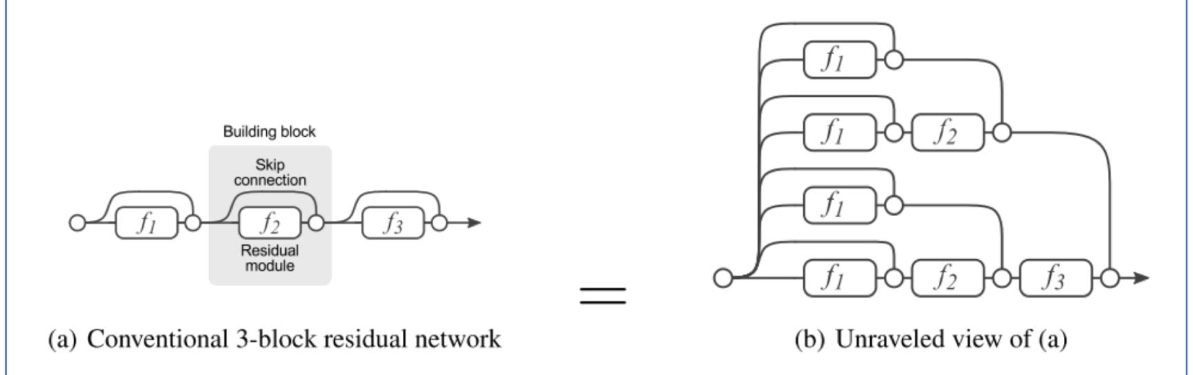
즉, 만약 f3에서 back propagation 진행 중, gradient값이 사라져도 skip connection을 통해 f2로 진행되고, 그 f2에서도 미분값이 사라지면 f1으로 바로 backpropagation을 진행해주면 된다.
이렇게 되면, 더 많은 layer를 중첩시킬 수 있게 되고, 깊이가 깊어질수록 성능이 향상되는 구조를 완성시켰다.
'학교공부 > [비디오이미지프로세싱]' 카테고리의 다른 글
| [비디오이미지프로세싱] - CNN(Convolutional Neural Network)_주요 Layer (0) | 2025.10.21 |
|---|---|
| [비디오이미지프로세싱] - Neural Networks (0) | 2025.10.18 |
| [비디오이미지프로세싱] - Linear Classification (0) | 2025.10.17 |
| [비디오이미지프로세싱] - 머신러닝(Linear Regression, Gradient Decsent) (0) | 2025.10.16 |



