1. 과목 개요
이번 학기에 졸업 프로젝트를 시작하면서, AI 쪽 기술, 특히 이미지 처리분야의 필요성을 느꼈다. 마침 3학년 2학기 때 본격적으로 학과 과정에 AI 관련 과목들이 개설되어, 수업을 들으며 거기에 그치지 않고 졸업 프로젝트와 연계하여 실제 문제 해결에 AI를 적용하기 위해 이 과목을 수강했다. 앞으로 이 과목을 통해 배운 내용을 정리하려고 한다.
2. 머신 러닝 Overview
사실, 4학년 2학기 전공으로 들어가 있는 과목이라, 기본적인 머신러닝이라는 개념을 알고 있다는 전제 하에 진행된다. 하지만 교수님께서 자세히 설명해 주셔서, 기본 개념부터 차근차근 정리할 수 있을 것 같다.
교수님은 머신러닝을 "함수 찾기" 또는 "함수 근사" 와 똑같은 말이라고 생각하면 된다고 하셨다. 그렇다면, 함수란 무엇일까? 지금까지 우리가 배워온 함수에는 크게 두 가지가 있다.
- 수학적 함수: 초등학교 시절부터 배웠던 입력과 출력 사이의 수학적 관계를 표현하는 함수
- 프로그래밍 함수: 코딩에서 사용하는 함수로 특정 입력을 받아 연산 후 출력을 반환하는 구조
두 함수의 공통점은 Input과 Output이 존재한다는 것이고, 이 둘 사이의 관계를 정의한다는 것이다. 머신러닝에서 말하는 함수도 같은 맥락에서 이해할 수 있고, 데이터로부터 이 함수를 찾는 것이 바로 머신러닝이라고 할 수 있다.
여기서 생기는 궁금증은 머신 러닝은 함수를 찾는 것인데, 어떻게 찾는 것일까? 이제부터, x를 Input, f(x)를 함수, y를 Output으로 사용할 것이다. 이전에 배웠던 함수들은, x와 f(x)가 주어지면 y를 찾는 과정이었다. 그렇다면, 머신러닝에서는 x와 f(x), y는 각각 무엇일까?
머신러닝에서 x는 다양하다. 이미지가 될 수도 있고, 긴 텍스트 형식이 될 수도 있고, 심지어 이미지+ 텍스트 형식이 될 수도 있다. 이 x에 대해서, f(x)에 넣으면 y가 나오는데, 다양한 y가 나올 수 있다. 몇 가지 사례들을 설명해 보면, 다음과 같다.
- 고양이 사진(x) > f(x) > 고양이 인식(y)
- 방 안 사진(x) > f(x) > 가구만 인식(y)
- 스카이 다이빙하는 사진(x) > f(x) > 사람의 몸 관절 움직임 그리기(y)
- 사진(x) > f(x) > 사진에 대한 글 설명(y)
- 꽃에 대한 텍스트 설명(x) > f(x) > 설명에 부합하는 꽃 사진 출력(y)
- 텍스트(x) > f(x) > 영어로 번역(y)
- 야구공을 던지는 사진 + 무슨 스포츠인지 알려달라는 텍스트형식 질문(x) > f(x) > 야구라고 답(y)
- 뇌 MRI 사진(x) > f(x) > 이상한 부분 탐지(y)
머신 러닝에서는 x,y를 찾는 것이 아니라 function 그 자체를 찾는 것이다. 즉, f(x)를 찾는 것인데, 어떻게 찾는 것일까? 먼저, x는 주어져 있다고 가정하고, 다음과 같이 4가지 방식을 다룰 예정이다.
- Supervised Learning: y가 주어져 있을 때
- Unsupervised Learning: y가 주어지지 않았을 때
- Weakly / Semi-supervised Learning: y가 일부분만 주어졌을 때(1,000,000개의 데이터 중 100개 정도만)
- Reinforcement Learning: 특정 actions set에 기반한 보상(rewards)으로 학습하는 방식
- ex) 한 단계 통과 > rewards, 통과 실패 > (-)rewards, 따라서 +쪽으로 조정될 수 있게
즉, 각 방식에 대해서, x와 y 또는 특정 값을 통해 f(x)를 찾아나아가는 방식을 머신러닝이라고 할 수 있다.
3. Linear Regression, Gradient Descent
앞서, 머신러닝에 대해서 정의를 해보았는데, 그럼, f(x)를 찾는 방식은 무엇이 있을까? 대표적으로 Linear Regression과 Gradient Descent가 있다.
이 방식들에 대해서 살펴보기 전에, 머신러닝에서 주어지는 데이터에 대해서 조금 더 자세하게 알아보자. 앞서, 머신러닝에서는 x, 즉 Input값으로 이미지, 텍스트, (이미지 + 텍스트) 등의 형식으로 주어질 수 있다고 했다. 그럼, 컴퓨터에서는 우리가 보는 그대로, 즉, 이미지 그대로 인식할까? 모두가 알고 있듯이 전혀 아니다. 즉, 컴퓨터는 숫자로 이루어진 데이터만 인식하기 때문에, 우리가 이미지로 값을 줘도, 그 이미지를 숫자로 변경해서 인식하게 된다.
예를들어, 아래 그림처럼 고양이 그림이 주어진다면, 컴퓨터가 인식하는 방법은 이미지의 특정 부분에 대해서 숫자로 인식한다.

즉, 이 숫자들을 벡터라고 부르고, 이미지 데이터는, 즉 컴퓨터에서 데이터는 벡터들의 집합으로 정의된다.
그리고, 만약 위 고양이 그림을 50x50x3의 숫자로 쪼깬다면, 즉, 총 7500개의 데이터로 표현할 수 있다. 이 이미지는 7,500차원 공간에서 한 점(datapoint)으로 표현된다고 볼 수 있다. 비록 직관적으로 7500차원이 상상이 안가지만, 개념적으로는 고양이 그림이 고차원 공간의 한 점으로 표현된다는 거싱다.
그럼 그림이 점으로 어떻게 바꿀 수 있을까? 바로 f(x), 즉 우리가 찾고자 하는 함수를 통해 이미지(x)값이 Datapoints(y)로 바뀌어서 표현되는 것이다. 즉, x(이미지) > f(x) > y(Datapoints) 로 표현할 수 있고, 목표는 이 f(x)를 찾아야 하는 것이다.
f(x)를 단순하게 1차 식으로 생각하고, f(x) = wx + b로 둔다. 이렇게 되면, 우리가 찾아야 할 값은 w와 b, 즉, f(x)의 기울기와 y절편이 된다. 그렇다면 이 둘을 구하는 방식 2가지 Linear Regression과 Gradient Descent에 대해서 알아보자.
- Linear Regression
Regression 방식은 일반적으로 데이터를 2차원 평면에 가져오고 그 위에 직선이나 2차 함수 이상의 그래프로 표현해 데이터를 설명한다. 따라서 이 방식으로 f(x)를 찾기 위해서는 x와 y는 real number(s)이어야 한다. 이 방식이 적용될 수 있는 예시들은 조금 제한적이다. 실제 숫자값으로 나타낼 수 있어야하는 데이터들이 필요하기 때문에, 다음과 같은 것들을 예시로 들 수 있다.
- 부모님 키와 자녀 키 사이의 관계 예측
- 단위 면적당 집값의 가격
- GPA와 공부 시간 사이의 상관관계
- CPU 속도와 프로그램 실행 시간 추정
- 가격과 음료 부피 크기의 상관관계 예측

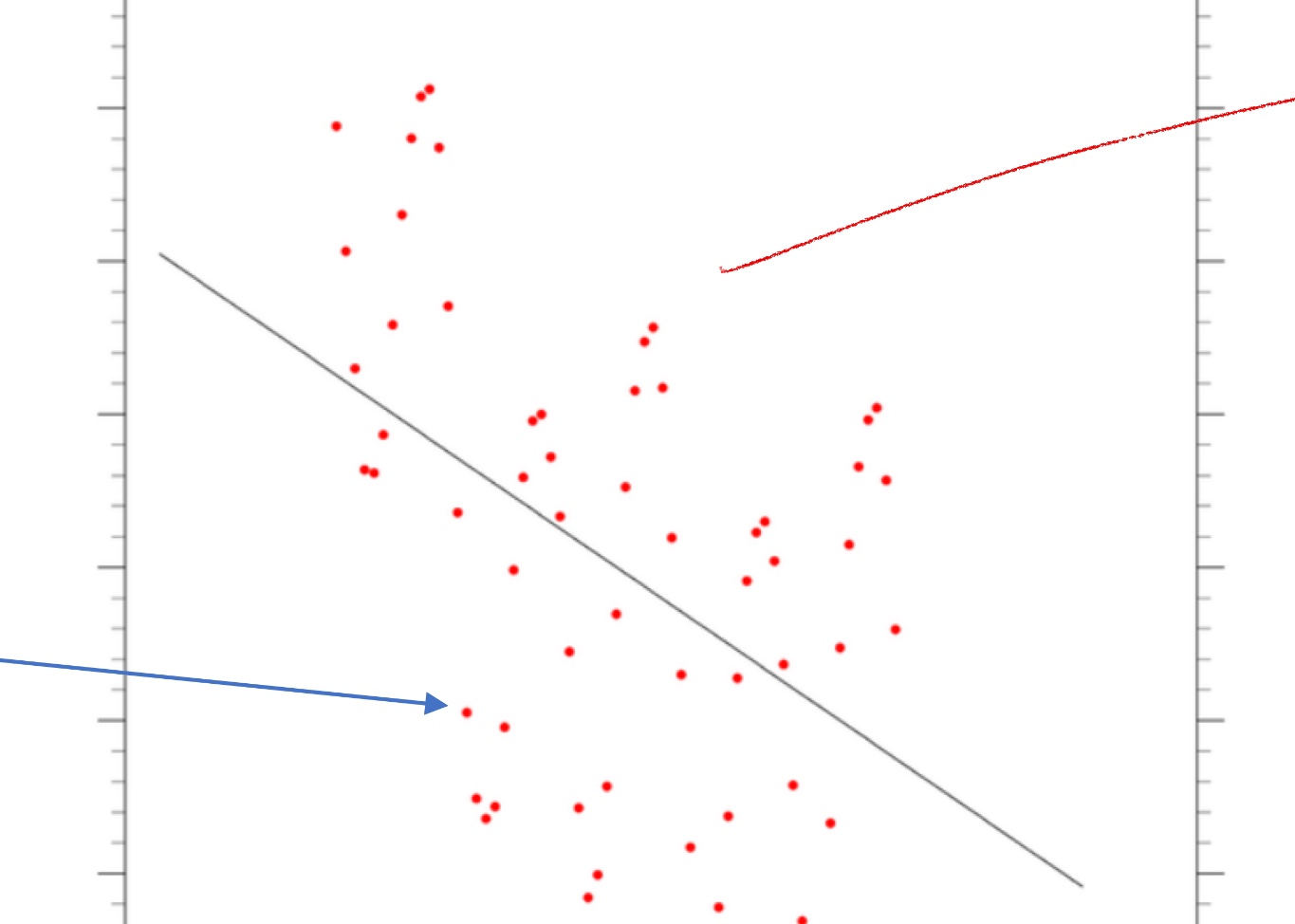
위 그래프는 키와 몸무게의 상관관계를 나타낸 표이다. 각 점들은 사람들의 키와 몸무게를 찍어놓은 데이터 set들이고, 이 데이터 set 사이에 존재하는, 대표값이라고 할 수 있는 빨간색 직선이 바로 우리가 찾아야하는 f(x)가 된다.
그럼 위 그림처럼, 실제 숫자들로 이루어진 데이터 셋들 중에서, f(x)를 찾는 방법은 어떻게 이루어질까? Linear Regression이라는 반복 알고리즘을 사용해 w와 b의 최적값을 구하는 것이다. 이 Linear Regression은 다음 그림과 같이 점을 먼저 찍은 다음, wx+b를 랜덤으로 초기값으로 잡아준 뒤, 데이터에 가까워지게 w와 b의 값을 조정해 주는 것이다.
예를 들어 다음 그림과 같이 5개의 x,y 데이터들이 존재한다고 가정하고 이에 해당하는 머신러닝 모델을 찾는다고 가정하자.

이때, 키=x, 몸무게=y라고 하고, 이를 대표하는 머신러닝 모델 f(x) = wx+b라고 두자. 이를 통해 f(x)를 찾게 되고, 만약 키가 165cm라는 입력값이 들어왔을 때, f(x)는 y=65라고 예측하게 될 것이다.
지금까지는 변수가 하나일 때의 경우만 다뤄왔다. 즉, x 하나로만 f(x)를 구성했지만, 실제로는 변수가 여러 개인 경우가 훨씬 많다. 따라서, 독립변수가 여러 개 존재할 때의 식도 당연히 필요하고, 이를 통해 식을 확장하면 다음과 같이 나타난다.
- f(x, y, z) = w0 + w1x + w2y + w3z
예를 들어, 총 판매량을 알고 싶고, 인터넷 판매량(변수 1), 모바일 판매량(변수 2), 오프라인 판매량(변수 3)이 존재한다고 하면 이때 독립변수가 3개에 의해 총 판매량이 달라지므로 모두 파악해야 한다. 즉, 이 경우도 간단히 독립 변수가 3개 존재할 때를 나타낸 것이다. 이때 우리가 구해야 하는 것은 w1,2,3값과 w0이다.이를 행렬곱으로도 표현할 수 있는데, 표현하면 다음과 같다.

이렇게 되면, 우리는 f(x) = Wx로 표현할 수 있게 되고, 이것이 바로 linear regression(=matrix-vector multiplication form)이라고 한다. 따라서 f(x) = wx+b 또는 f(x) = Wx로 표현되는 모든 함수는 linear regression이라고 할 수 있다.
그러면 실제로 이 linear regression이 어떻게 적용되고 구할 수 있는지 알아보자. 다음과 같은 학습 데이터가 있다고 가정해보자.

이 세점을 대표하는 직선은 무수히 많을 것이다. 그럼 우리의 목표는 linear regression을 통해 세 점을 가장 잘 설명하는 f(x) = wx + b를 찾는 것이다.
이전까지는, 우리는 찾고자하는 미지수가 2개일 때, 식은 2개만 존재하면 됐다. 그렇지만, 이 경우, f(x)에 학습시킬 데이터는 3개로, 총 3개의 식이 나온다. 만약, 우리가 3개의 식 중 2개의 식만으로 f(x)를 찾는다면, 원하는 f(x)를 얻지 못할 수도 있다. 즉 다음과 같은 경우이다.

예를 들어, 우리가 실제로 찾고 싶은 f(x)는 빨간 색인데, 만약 (1,2), (2,5)로 나타낸 식으로만 f(x)를 찾는 다면 엉뚱한 f(x)인 파란 색으로 구할 수 있다는 것이다. 사실, 이 경우는 찾고자 하는 f(x)와 별 차이는 없지만, 만약 학습시킬 데이터가 여러 개 존재하거나 값 차이가 크다면 그래프 간 오차도 커질 것이다. 결과적으로, 우리가 입력값을 넣었을 때, 예측값이 아예 다르게 나올 수 도 있게 되고, 학습의 의미가 없어지게 된다.
따라서, 우리는 최대한 많은 데이터를 이용해 데이터들을 대표할 수 있는 가장 일반화된 f(x)을 찾아야 하며, 모든 데이터들을 다 지나치는 그래프보다는 최대한 대표할 수 있는 f(x)를 찾아야 한다는 것이다. 즉, 머신러닝에서 y = f(x)를 구하는 것은 매우 힘들고, y ≈ f(x)를 찾아야 한다.
즉, 최종적으로 우리는 y와 f(x)의 차이를 최소화시키는 f(x)를 찾는 것이 목표이다. 그 중 대표적인 방법 하나는 오차의 제곱 값을 통해 구하는 것이다. 즉, (y - f(x))^2값을 최소화하도록 최적의 w(기울기)와 b(y절편)를 찾는 것이다. 위의 데이터들을 적용해서 구하는 방법은 다음과 같다.
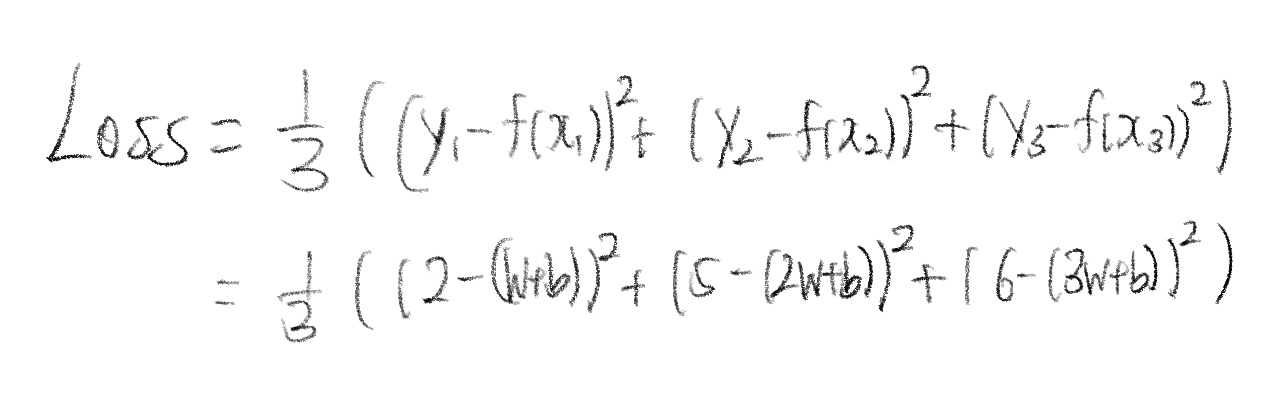
Loss에 관한 식을 조금 더 설명하면 다음과 같다.
- 주어진 학습시킬 데이터들을 각각 (x1,y1), (x2,y2), (x3,y3)라고 하고, 각각을 이용해 w와 b에 대한 식으로 나타낸다.
- 이 때, 1/3은 3개 값의 평균을 나타내는 것인데, 평균이 값을 대표하는 값 중에 하나이기에 이 평균은 해도되고 안해도 된다.
즉, 이렇게되면 w,b에 대한 이차 방정식으로 Loss가 표현되게 되며, 이를 일반화 시키면 다음과 같다.
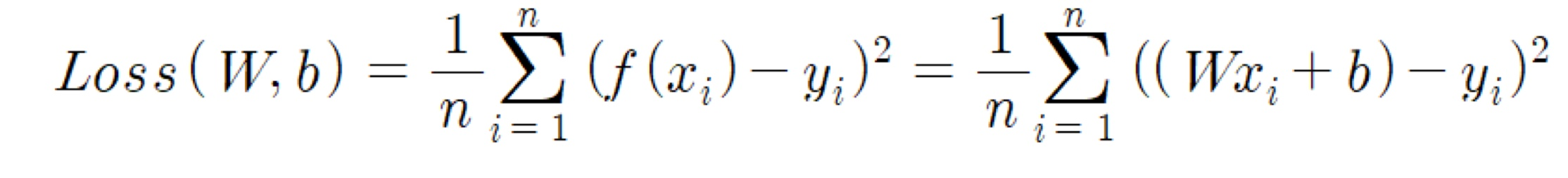
이렇게 Loss를 구하고, 이 Loss를 최소로 만드는 w,b를 구하면 된다. Loss를 최소로 만드는 w,b를 구하기 위해선 위 식을 각각 w에 대한 이차방정식으로 생각하고 w의 최솟값(미분을 통해 구할 수 있다)과동일하게 b에 대한 이차방정식으로 보고 b의 최솟값을 구하면 된다. 즉, 이를 일반화시킨 식으로 나타내면 다음과 같다.
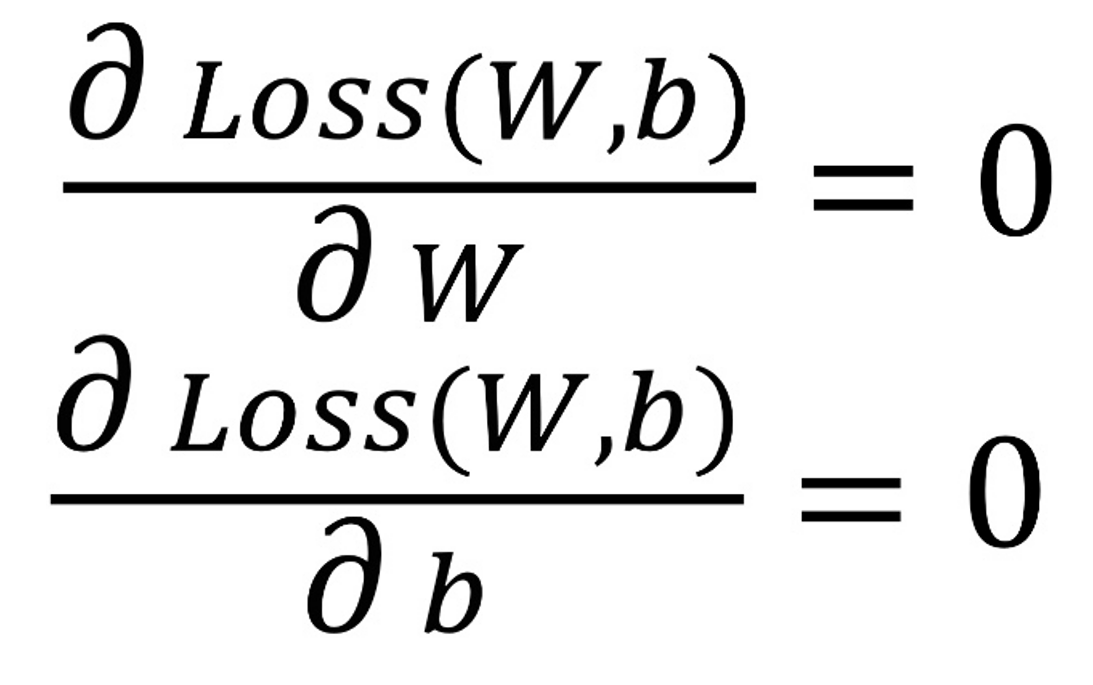
그렇지만 이 방법에는 한계가 존재한다. 기본적으로, 위 식을 통해서 구할 수 있다는 것은 Loss 함수가 미분 가능해야된다. 하지만 실제로는 sin, cos, 지수함수, 로그함수 등으로 표현되는 복잡한 모델이 많고, 이런 경우에는 미분이 어렵거나 불가능하기 때문에, 쉽게 계산되지 않는다.
- Gradient Descent
따라서 위 Linear Regression 방식의 한계점을 극복하기 위해 등장한 방법이 바로 Gradient Descent 방식이다. 이 방식은 간단하게 설명하면 Iterative optimization algorithm(반복적 최적화 알고리즘)이다. 즉, Linear Regression의 기본 원리를 반복적으로 갱신하여 점차 최적값에 수렴하도록 개선한 알고리즘이다.
기본적으로, Linear Regression 방식을 따르기 때문에 Loss Function은 동일하다. 즉, 위에서 정리했던 다음과 같은 Loss 함수를 사용한다.
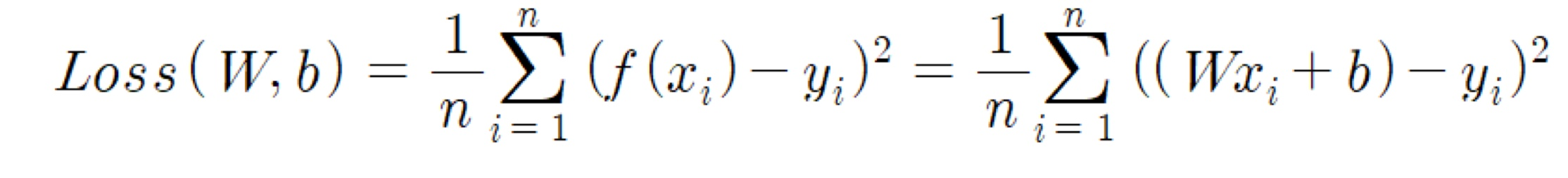
결과적으로 이 식은 2차 함수로 표현되는 식이기 때문에 여기서 Gradient Descent의 아이디어가 출발한다.
- Loss가 최소화가 되기 위해서는 이차함수에서 최솟값을 찾으면 된다.
- 해당 최솟값은 미분했을 때 값이 0이되는, 즉, 기울기가 0이 되는 부분에서 Loss가 최솟값을 갖는다.
따라서, Loss에 대한 함수의 미분값들을 구해보며,
- 해당 값이 0보다 작으면 값이 커지는 쪽으로,
- 해당 값이 0보다 크면 값이 작아지는 쪽으로 조정을 해준다는 것이다.
그리고, 만약, 미분값이 0이 된다면 업데이트를 멈추고, 해당 지점에서 w,b를 구하면 된다는 것이다.
이 Gradient Descent 방식은 인자가 몇 개 존재하던지, 즉 독립 변수의 개수와 상관없이 모든 f(x)에 대해서 적용할 수 있다. Loss를 최소화 하는 W를 구하는 식을 일반화시키면 다음과 같다.

이 식에 대해서 설명하면 다음과 같다.
- W(n) = 현재 단계에서 가중치 값
- W(n+1) = 그 다음 단계의 가중치
- γw = Learning Rate(=학습률)로 얼마나 많이 빠르게 이동할지 결정
- 미분식 = Loss를 W에 대해 미분한 값 = 기울기
따라서, 결과적으로, 다음 가중치를 업데이트 하는 방법은 이전 가중치에서 미분값을 빼는 것인데, 미분값을 빼주는 이유는 0과 가깝게 움직이게 하도록 위해서이다.
- Gradient Descent의 한계점
Gradient Descent 방식이은 매우 보편적이지만, 모든 기계학습의 모델에 완벽히 적용되는 것은 아니다.
먼저, Learning rate에 대한 문제다. Learning rate은 컴퓨터가 자동으로 설정해주는 값이 아닌 모델을 만드는 사람이 설정해줘야 하는 상수 값이다. 이 값을 적절하게 조정하지 않으면, 다음과 같은 문제가 발생한다.
- 만약, learning rate을 너무 낮게 설정한다면, 기울기가 0이 되게 하기 위해서 너무 많은 연산을 진행해야 되고, 찾는 데 시간이 오래 걸리는 문제점이 발생한다..
- 또 그렇다고 해서 너무 높게 잡게 된다면, 안정적으로 수렴하지 못하고, 오히려 Loss가 발산하게 될 수도 있다.
따라서, Learning rate을 적절하게 조절해줘야 한다.
또 다른 문제점은 Local Mininma Problem이다. 다음과 같은 Loss 함수가 나왔다고 가정하자.
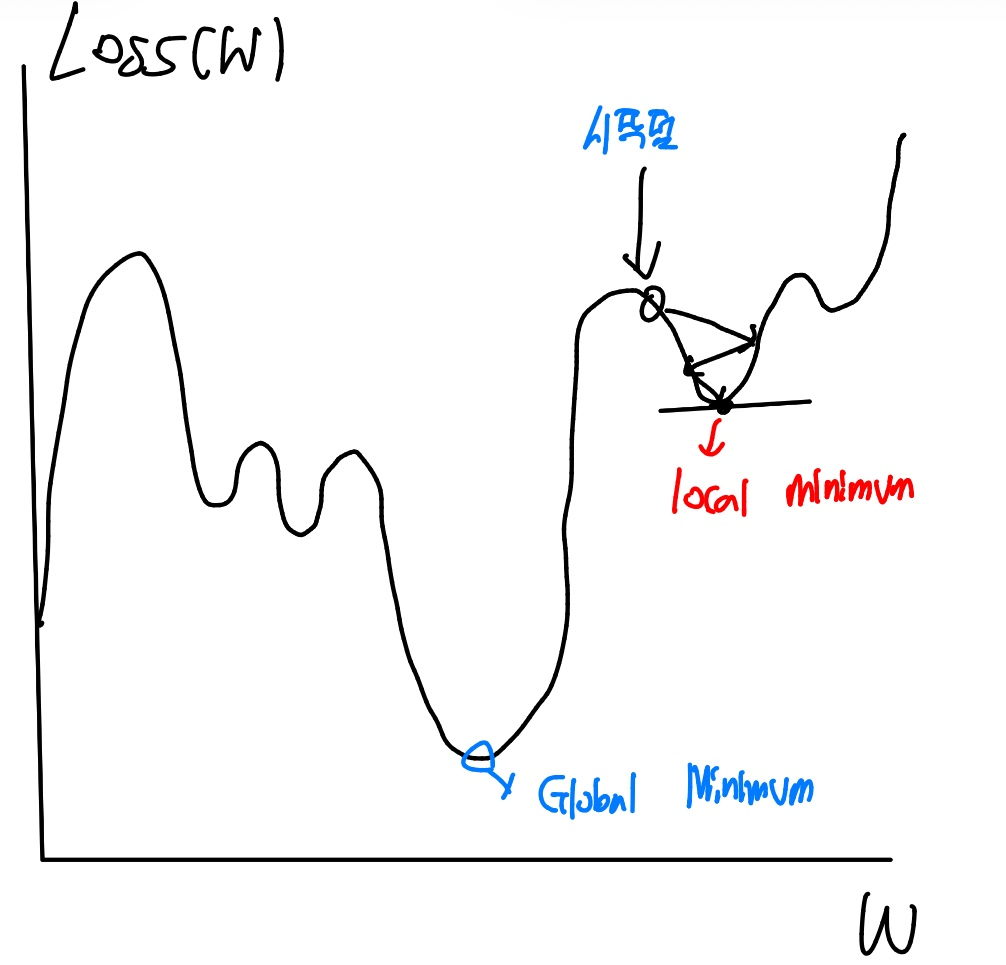
이 경우는 복잡한 Loss 함수에 대해 미분값이 0 인 부분이 여러 개 존재하게 된다. 그렇기에 시작점을 위 그림과 같이 잡게 되면, 이 함수 전체에서 최솟값이 아닌 해당 지역에 해당하는 최솟값, local minimum이 나오게 된다.
이러한 문제는 아직 해결되지 않았지만, 일반적으로 local minimum도 최솟값이기 때문에 실제 모델에서는 이를 그대로 활용하는 경우도 많다.
정리하자면, 우리는 Linear Regression, 또는 Gradient Descent 방식으로 데이터들을 잘 나타내는 f(x)를 찾거나, 해당 f(x)를 통해 데이터를 분류(구분)할 수 있다.
이 Gradient Descent 방식의 차원을 조금 더 확장해보자. 이때까지는 Gradient Descent를 표현할 때, Loss와 W(가중치), Loss와 b(bias) 두 관계를 따로 따로 나타냈다. 그렇지만, 따지고 보면, Loss는 W와 b에 의해서 값이 변하기 때문에 이를 3차원으로 확장하면, w,b, loss에 대한 관계가 다음과 같이 표현된다.

이를 또, 위에서 수직 방향으로 바라보면, 다음과 같이 등고선 형식으로 나타낼 수 있다.

따라서, Loss는 등고선처럼 생긴 가운데 부분에서 최솟값을 가지며, 이 값에 가깝게 w와 b를 각각 조정해줘야 한다.
결국, W와 b를 따로 각각 계산해주어 loss가 줄어드는 방향으로 계산해야 되는 방식은 동일하다. 만약, f(x)가 다음과 같이 벡터(행렬)로 표현된다고 가정해보자.

이렇게 되면, w11에 대한 가중치, w12에 대한 가중치, w13에 대한 가중치..에 대해 모두 업데이트를 해줘야 한다. 이렇게 되면 연산이 너무 많아져 컴퓨팅 시간 뿐 아니라 자원 할당에도 비효율이 생긴다.
- Stochastic Gradient Descent(SGD)
위와 같은 Gradient Descent 문제를 해결하기 위해 등장한 방법이 바로 Stochastic Gradient Descent이다.
이 방법은, 학습시킬 데이터가 엄청나게 많을 때, 연산이 엄청나게 많이 일어날 Gradient Descent를 대신해서 학습시킬 데이터들을 쪼개서 각각에 대해서 Loss를 반복해서 계산하는 방식이다.
예를들어, 학습시킬 데이터가 100,000개라고 가정해보자. 이를 Gradient Descent로 한 번에 학습시키는 경우, 컴퓨터 계산량이나 자원 할당에서 비효율적이다. 때문에 SGD는 이 100,000개의 데이터를 mini-batch로 쪼개는 것이다. 하나의 mini-batch에 1000개씩 담는다면, 총 100개의 mini-batch가 생기게 된다. 그리고 각 batch에 대해서 Gradient Descent방법을 적용하여 Loss를 계산하고 기울기 방향에 따라 W와 b를 반복적으로 조정해주면 된다.
다른 예시를 한 번 생각해보자. 만약, 찾아야 할 모델이 f(x) = wx+b로 표현되어 있고, 실제 찾아야 하는 모델을 다음과 같이 평면에 표현되어 있다고 가정해보자.
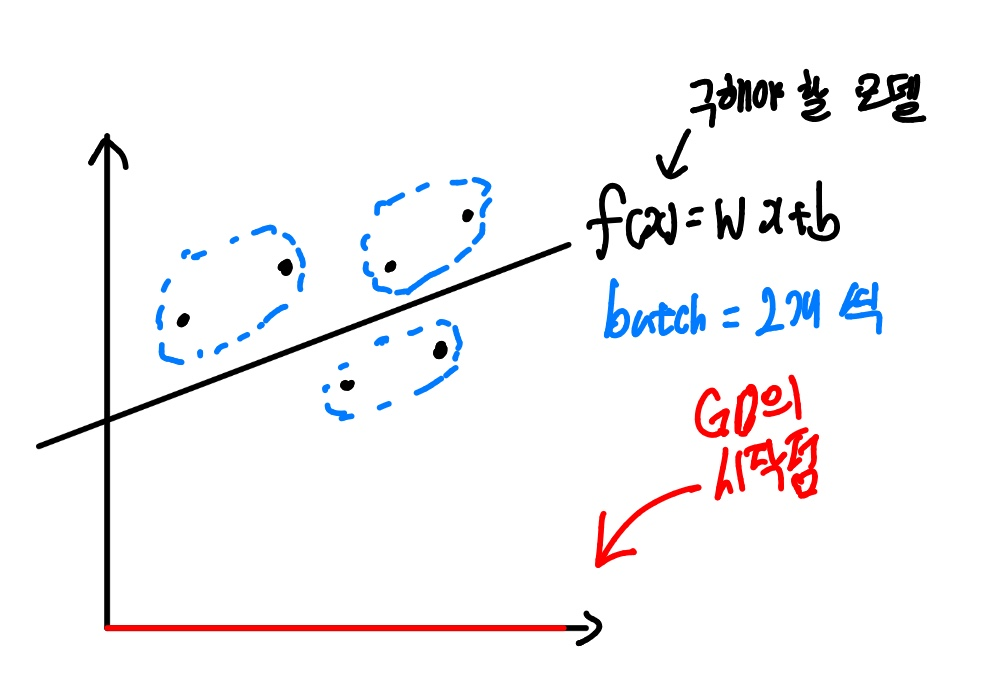
이때, 이 그림에 대해서 설명하면 다음과 같다.
- 데이터는 6개로, 좌표평면 상에 점으로 표현되어 있다.
- SGD로는 batch크기를 데이터 2개로 잡고, SGD는 b=0에서 시작한다.
만약, SGD로 실행한다면 다음과 같이 진행될 것이다.
- W=0, b=0에서 첫 번째batch(데이터 2개)로 Loss를 계산하고, 기울기에 따라 W,b를 업데이트 한다.
- 갱신된 W,b를 사용해 두 번째 batch의 Loss를 계산하고 다시 업데이트한다.
- 해당 작업을 한 번 더 반복한다.
이 과정을 거치면, 모델 f(x) = wx+b로 점점 더 가까워 지게 된다. 반면, GD 방식으로 진행한다면, 모든 6개의 데이터를 한 번에 사용하여 전체 Loss의 최솟값을 한 번에 계산하게 될 것이다.
이를 아까 표현했던 등고선으로 표현하면 다음과 같게 진행될 것이다.


왼쪽은 SGD, 오른쪽은 GD 방식으로 진행할 때, 최솟값으로 수렴하는 과정을 등고선으로 표현한 것이다.
이때, 왼쪽 SGD 방식을 잘 보면, 최솟값으로 도달할 때까지 화살표의 방향이 계속 바뀌는 것을 볼 수 있다. 이는 각 batch마다 Loss값을 최소화하는 방향이 조금씩 다르기 때문이다. 즉, SGD는 매 batch마다 Loss가 최소가 되는 방향으로 이동하므로, 경로가 불규칙하게 흔들린다. 그리고, SGD는 최솟값 근처에 도달했을 때, 진동(oscillates)하는 특징이 있다. 즉, 마지막에 최솟값에 가까워져 Loss값을 최소화 하려면 많이 움직이지 못하고 쪼금쪼금씩 움직이는 것이다.
반면, 오른쪽의 GD는 전체 데이터를 한 번에 고려해서 계산하기 때문ㅇ Loss의 최솟값으로 매끄럽게 수렴하여 이동한다. 즉, SGD와 달리 비교적 안정적으로 최소값에 다다를 수 있다.
그렇다면 SGD와 GD를 비교했을 때, 최솟값에 안정적으로 도달하는 면에 있어서 GD를 쓰는게 낫지 않나 라는 의문이 생길 수 있다. 그럼에도 계산하는 속도가 SGD가 훨씬 빠르고, 진동을 하면, 경우에 따라서는 Local minimum도 벗어날 수 있는 장점도 있다. 따라서, 실제 머신러닝과 딥러닝에서는 약간의 진동이 있더라도 학습 속도와 효율성이 높은 SGD를 대부분의 모델에서 사용한다고 한다.
'학교공부 > [비디오이미지프로세싱]' 카테고리의 다른 글
| [비디오이미지프로세싱] - CNN_Activation Functions (0) | 2025.10.22 |
|---|---|
| [비디오이미지프로세싱] - CNN(Convolutional Neural Network)_주요 Layer (0) | 2025.10.21 |
| [비디오이미지프로세싱] - Neural Networks (0) | 2025.10.18 |
| [비디오이미지프로세싱] - Linear Classification (0) | 2025.10.17 |



