지난 글에서는 Neural Network 기본 개념과 그 핵심 작동 원리인 forward propagation, backward propagation에 대해서 알아보았다. 또한 마지막에는 Nerual Network의 발전 과정과 CNN(Convolutional Neural Network)의 기반이 된 VGGNet에 대해서 정리해 보았다. 이번 글에서는 CNN이 정확히 무엇이고, 어떤 방식으로 이미지 데이터를 처리하는지 한 번 정리해보려고 한다.
1. CNN(Convolutional Neural Network)의 활용 분야
CNN은 이름에서도 알 수 있듯이 기본적으로 Neural Network의 한 종류이다. 즉, 여러 Layer(함수)를 쌓아 학습한다는 점에서는 기존 Neural Network와 동일하지만, Convolution(합성곱) 연산을 통해 feature를 추출한다는 점이 가장 큰 차이점이다.
이러한 구조 덕분에 CNN은 시각적 데이터를 다루는 데 매우 유리하며, 현재 다음과 같은 다양한 분야에서 활용되고 있다.
- Classification(분류): 이미지가 어떤 클래스에 속하는지 판별
- Detection(사물 탐지): 이미지 내에서 객체의 위치와 종류를 인식
- Segmentation(분할): 픽셀 단위로 이미지를 구분하여 객체의 영역을 추출
- Game AI: 비디오 게임에서 활용
- Arts: 사진을 특정 화풍으로 변환하고 싶을 때 활용
2. CNN - AlexNet 작동 원리
지난 글에서, AlexNet, 숫자 손글씨 인식 모델에 대해서 정리할 때, CNN의 시초라고 했다. 그래서 CNN이 어떻게 동작하는지 이해하려면, AlexNet이 먼저 어떻게 작동하는지 알아야하는데, 다음과 같이 작동한다.
- 손글씨 사진이 Input으로 들어온다.
- (Conv + Pool)로 이루어진 layer 2개를 통과한다.
- 이 후 추가적으로 Conv로만 이루어진 Layer나 (Conv + Pool)로 이루어진 Layer를 몇 개 통과한다.
- 2번의 FC layer를 거치고(각 클래스에 대한 점수를 계산)
- 최종적으로 Softmax layer를 거쳐 각 클래스별 확률을 계산한다.
Softmax까지 거치면, A일 확률 0.2, B일 확률 0.8, ... 처럼 어떤 클래스일 확률이 높은지를 벡터 형태로 출력한다.
3. CNN의 주요 Layer
앞서 AlexNet의 과정에서 등장했던 Conv, Pool, FC, Softmax layer는 무엇일까? 이 Layer들에 대해서 이제 알아보려고 한다.
- FC(Fully Connected) Layer
먼저 알아볼 Layer는 FC(Fully Connected) Layer이다. Fully Connected는 Softmax Layer 전, 즉, 최종 출력 직전 주로 2번 사용되는 Layer인데, 그 구조와 원리를 한 번 알아보자.
FC Layer는 입력값이 이미지의 height, width, channels 이다. 즉, M*N*P 형태이다.
하지만 이 이미지를 FC Layer에 통과시켰을 때, 결과는 1차원 벡터이다. 따라서, FC Layer를 통과하기 전 입력값을 1차원 벡터로 평탄화해주는 과정을 거친다. 다음 그림을 한 번 살펴보자.
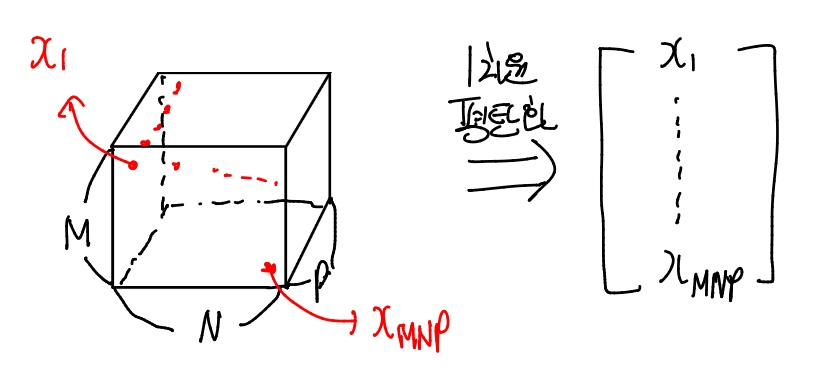
즉 출력값이 1차원 벡터이기 때문에, 입력갑인 이미지를 1차원으로 평탄화로 진행해준 다음 FC Layer의 연산이 진행된다.
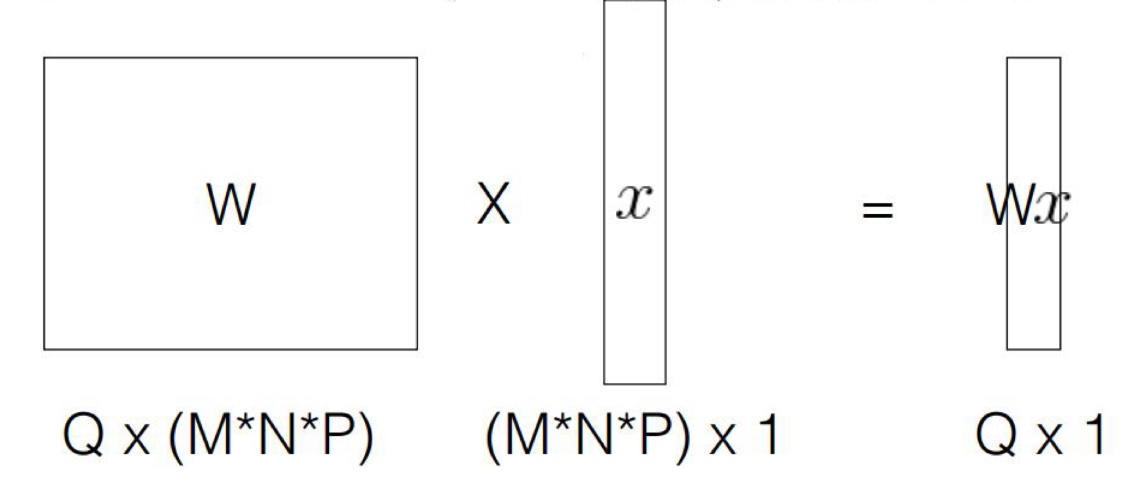
출력의 크기(차원)는 모델 설계자가 자유롭게 설정할 수 있다. 출력 벡터의 차원을 Q라고 하면, FC Layer 연산은 다음과 같은 식으로 표현할 수 있다.
y = Wx
- W: Q x (MNP) 크기의 가중치 행렬
- x: 평탄화된 입력 벡터((MNP) x 1)
- y: 출력 벡터(Q x 1)
즉, 흔한 Linear 함수 Wx를 통해 Output을 결정하는 것인데, W는 Q x (M*N*P)의 벡터, x는 위에 나타낸 것처럼 이미지를 1차원으로 평탄화 시킨 벡터이다. 이 둘의 내적(= 행렬 곱)을 통해 Output을 계산한다. 이때, W는 학습이 이미 완료된 대상이다. 이때, Output의 하나의 벡터를 계산하기 위해서는 다음과 같은 내적을 진행해야한다.
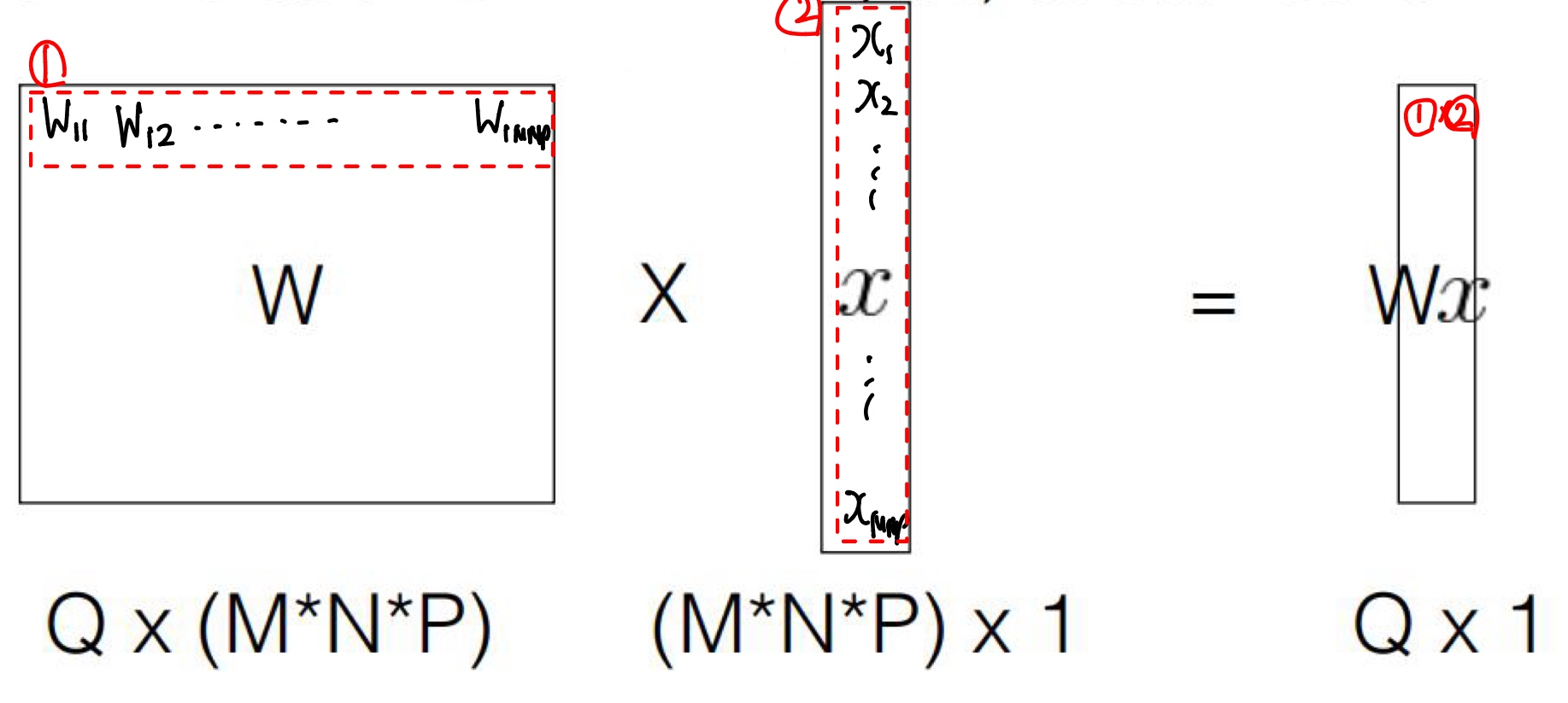
즉, W와 x의 모든 값들을 서로 내적해 Output을 구하기 때문에 Fully Connected Layer라고 부른다.
이런 FC Layer는 약점이 존재한다. 입력 크기가 커진다면, 계산이 그만큼 늘어난다는 것이다. 예를 들어, 입력이 200 * 200 * 1이라고 하자. 입력 벡터(x)의 길이는 40만 개가 된다. 이때 출력 크기 Q가 1000이라면, 필요한 W(가중치)의 수는 4억 개가 된다.
이처럼 매우 많은 연산량과 메모리 사용량이 발생하므로, FC Layer는 보통 입력이 충분히 축소된 마지막 부분에서만 사용된다. 예를 들어 AlexNet의 구조에서도 초기에서는 Convolution과 Pooling을 반복하여 공간 크기를 줄인 후, 마지막 단계에서만 FC Layer를 2회 사용한다. 즉, FC Layer는 요약된 특징을 최종적으로 결합하고 분류하는 단계로 활용된다.
- Convolutional Layer
다음으로 알아볼 Layer는 Convolutional Layer이다. 앞서 배운 FC Layer에서는 입력값이 크기가 너무 크면 계산량이 급격히 증가하므로, 입력을 충분히 축소시켜야 한다는 점을 확인했다. 그렇다면 이 원본 이미지를 어떻게 축소시킬 수 있을까? 이 과정을 담당하는 것이 바로 Convolutional Layer이다.
- Convolution(합성곱)
Convolutional Layer는 Convolution(합성곱)이라는 개념이 적용되는데, 이 Convolution은 그럼 무엇일까? 예를 들어 다음 상황을 가정해보자.
- 6 x 6 크기의 입력 이미지와 3 x 3의 필터(또는 커널)가 있다고 가정해보자.

이때, 3*3의 필터는 6*6 이미지에서 좌측 상단에서 시작해 오른쪽과 아래쪽으로 한 칸씩 이동하며 겹치는 부분의 값들을 곱한 뒤, 모두 더하는 연산을 수행한다. 이 과정을 이미지 전체에 반복하면, 출력은 4*4 크기로 만들어진다. 즉, 입력 6*6이 4*4로 크기가 줄어들며, 이러한 과정을 Convolution 연산이라고 한다.
이 Convolution 연산에서, filter가 입력 위를 이동(slide)하는 방법이 여러가지 있는데, 수업에서 다룬 내용은 다음과 같다.
- Stride 1: 기본 옵션으로, 옆으로 이동할 때 1칸씩, 아래로 이동할 때도 1칸씩 움직이며 계산하는 방법
- 세밀한 특징을 잡아내지만, 출력 크기가 커진다.
- Stride 3: 이동할 때 3칸씩(옆이든, 아래로든) 움직이며 계산하는 방법
- 연산량이 줄고 출력 크기가 작아지지만, 세밀한 정보는 떨어질 수도 있다.
즉, Stride 값이 커질수록, 출력 크기는 작아지고, 연산량이 줄어드는 대신, 정보 손실 가능성이 커진다.
- Convolutional Layer 동작 원리
그럼 이제, 본격적으로 Convolutional Layer는 어떻게 동작하는지 한 번 알아보자. 다음과 같은 예시가 있다고 가정해보자.
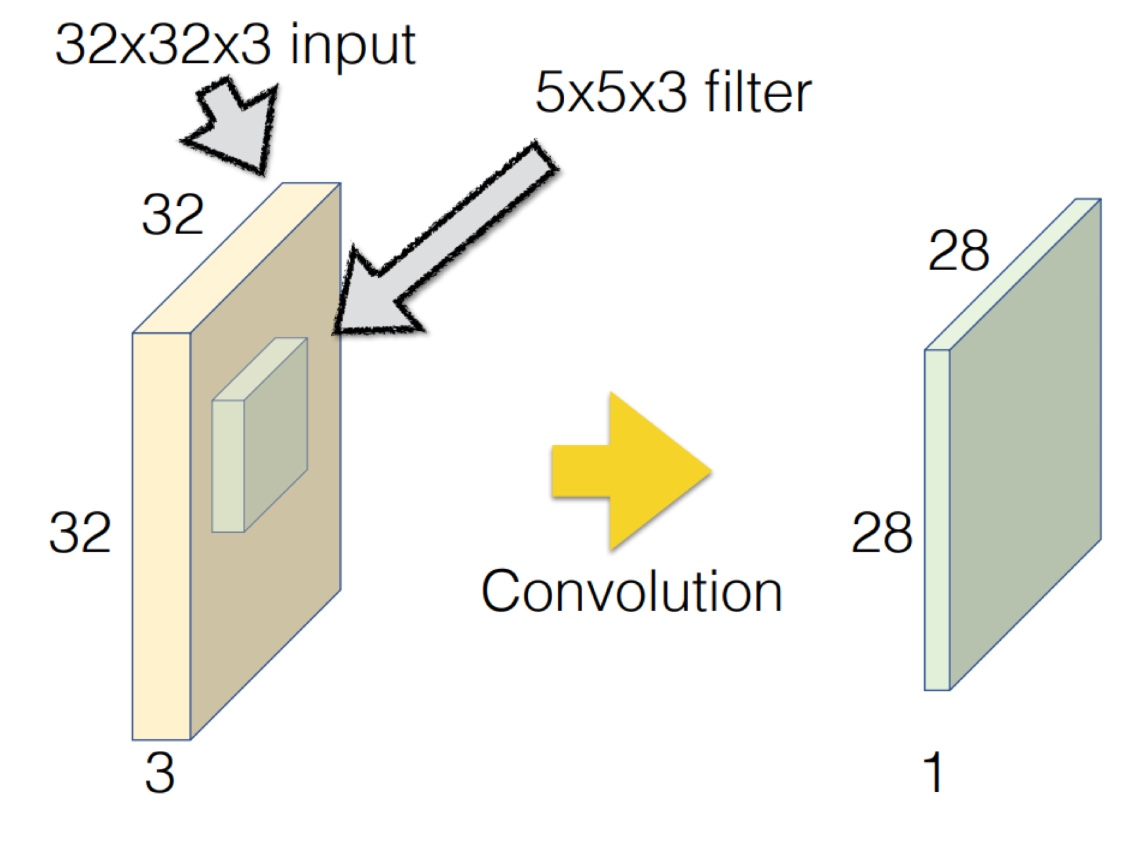
그림에 대해서 설명하면,
- 32x32x3의 이미지 입력값과, 5x5x3의 필터(커널)를 선택했다.
여기서 필터를 선택할 때는, 입력의 채널 수(3)과 동일해야 한다. 즉, RGB 이미지(3채널)에서는 필터의 채널도 3이어야 각 채널에 대한 정보를 동시에 반영할 수 있다. 이렇게 Convolution 계산을 진행해주면, 출력의 크기는 28*28*1이 된다.
이때, Convolution Layer에서는 하나의 필터로만 진행하지 않고, 여러 필터를 사용해 여러 출력을 구한다. 예를 들어, 4 5*5*3(4개의 5*5*3의 필터를 사용했다는 뜻)으로 총 28*28*1의 output을 4개 얻었다.
필터를 여러 개를 사용하는 이유는 입력 데이터의 다양한 특징을 학습하기 위해서이다. 예를 들어 사람 얼굴을 인식하는 모델을 학습한다고 하자. 하나의 필터만 사용한다면, 얼굴의 위치를 왼쪽으로 5px만 이동해도 얼굴 인식이 실패할 수도 있다.
이러한 문제를 막기 위해서 우리는 학습시킬 때, 여러 필터를 사용한다.
- 얼굴을 Input이라 했을 때, 우리는 3개의 필터를 사용한다고 가정해보자.
- 3개의 필터는 각각 눈, 코, 입 필터라고 가정하자.
- 입력 이미지에 대해 각 필터를 적용하면, 눈 필터를 거치면 눈이 있는 위치에서 높은 값을 가질 것이고, 코 필터는 코 위치에서, 잎 필터는 입 위치에서 높은 값을 가질 것이다.
이제 이 결과를 종합하여 세 부분이 모두 감지되면(세 결과의 합이 3이상이 된다면) 얼굴로 인식하는 모델을 학습할 수 있다. 이처럼, 여러 필터를 사용함으로써 서로 다른 특징(엣지, 윤곽 등)을 동시에 학습하고 인식할 수 있게 된다.
- Zero-padding과 Output size
Convolution 연산을 반복하다 보면, 필터가 입력 이미지의 가장자리(edge)를 제대로 커버하지 못한다. 이를 방지하기 위해, 또, 크기가 너무 지나치게 작아지지 않게 하려고 입력 테두리에 0 값을 추가하는 것을 Zero-padding이라고 한다.
예를 들어, Zero-padding이 2라면 입력의 상하좌우에 2칸씩 0을 덧붙여 입력 크기를 확장시킨 뒤 연산을 수행한다. 이렇게 하면 출력 크기가 너무 작아지지 않게 조절할 수 있고, 가장자리 정보도 더 잘 보일 수 있다.
이 zero padding의 경우, output size를 어떻게 유추할 수 있을까? 다음과 같은 상황을 가정해 보자.
- Zero-padding = 2, Input size = 4*4*2, Kernel size = 2*2*2, Stride = 1
이때, 차례대로 p, i, k, s라고 하면, Output size는 다음과 같은 식으로 나타낼 수 있다.

이 식을 통해 위 상황의 Output size를 계산해보면, (4+2*2-2)/1+1 = 7로, Output size는 7*7*2로 유추할 수 있다.
+) 추가로, dilaition(팽창) 개념을 적용할 수 있다. Dilation은 필터 내부의 간격을 인위적으로 벌려 더 넓은 범위의 입력 정보를 한 번에 인식할 수 있게 하는 방법이다. 이렇게 되면, 한 번의 Convolution으로 볼 수 있는 입력의 범위가 넓어진다. 다음 그림을 참고하자.
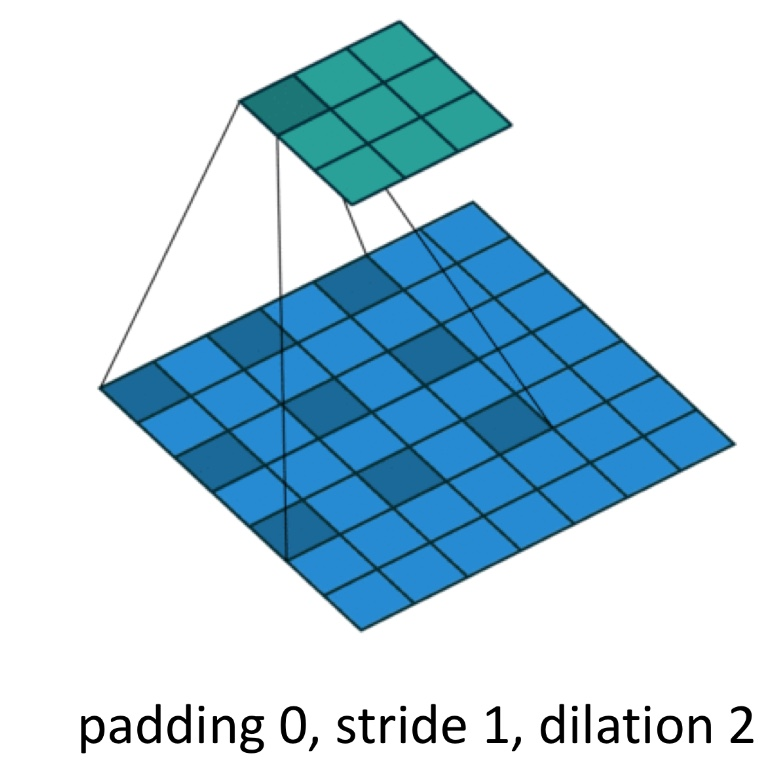
- Transposed Convolution
이번에는 조금 특이한 Convolution, Transposed Convolution에 대해서 정리해 보려고한다.
일반적인 Convolution Layer는 입력의 크기를 줄여 다음 Layer(특히 FC Layer)에 더 작은 입력을 전달하는 역할을 한다.
하지만, Transposed Convolution은 반대로 작은 입력을 다시 큰 크기의 출력으로 복원하기 위한 연산이다.
그럼 크기를 키우려면 어떻게 해야할까? 다음과 같이 두 가지 방법이 존재한다.
- Filter의 크기를 키운다.
- 한 번의 연산으로 더 넓은 영역을 커버해 출력의 공간 크기를 확장한다.
- Padding 값을 늘려준다.
- 입력보다 필터가 커질 경우, 필터가 입력의 테두리르 벗어나지 않도록 추가적인 Zeor-padding을 해준다.
결과적으로, Transposed Convolution은 필터와 패딩을 조합하여 출력의 공간 크기를 늘리는 방식이다.
이런 경우에는, Output size를 계산하는 방식도 다르다. Output size를 계산하는 방법은 다음과 같이 바뀐다.

확장하는 방법을 그림으로 표현하면 다음과 같다.

- Pool(Pool layer)
다음으로 알아볼 Layer는 Pool Layer이다. Pool Layer는 Convolutional Layer로부터 얻은 특징 맵(feature map)의 크기를 줄이는 역할을 한다. 보통 Convolution Layer 다음에 사용되고, 채널 수를 유지하고 공간 크기만 줄인다.
이 정의만으로는 이해가 잘 안 될 수 있다. 위에서랑 마찬가지로 사람 얼굴을 탐지하는 모델을 학습한다고 가정해보자. 사람의 이미지를 넣으면, Convolutional Layer에서는 눈, 코, 입 필터를 통해 눈만 남기고, 코만 남기고, 입만 남기는 feature map(특징 맵)을 만든다. Pool Layer에서는 이 특징 맵을 "요약"하는 역할을 한다.
그럼 이 요약은 어떻게 진행될까? 제일 흔하게 사용되는 Max Pooling을 통해 알아보자. 한 Feature Map이 다음과 같이 생겼다고 가정해보자.

이를 Pool Layer를 적용해 "요약"하려고 한다. 이때, 요약하려는 것은 곧 축소를 의미하기에 Pool Layer에도 필터가 존재한다. 이 예시에서는 3*3 크기의 필터와 Stride 2 기법을 적용해 Max Pooling을 이용할 것이다. 이렇게 되면, 다음과 같이 진행된다.

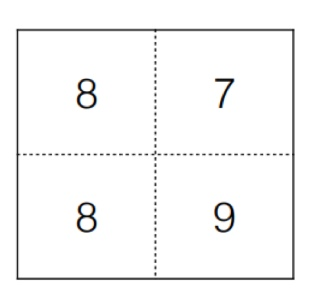
즉, 필터가 총 4번 훑게 되는데, 그 필터 내 영역 중 최댓값을 결과에 적는 것이다. 따라서 처음에는 8, 다음은 7, 그 다음도 8, 마지막에는 9가 결과값에 적히게 된다. 이렇게 하면, feature의 특징을 그대로 살리면서 크기를 확 줄일 수 있게 된다. 이를 요약한다고 하는 것이다.
예를 들어, 얼굴 사진이 들어와서 Convolutional Layer에 눈 필터를 적용해서 눈이 있는 위치만 1, 나머지는 다 0이 저장되는 feature map이 만들어진다고 가정하자. 그럼 이를 전달받은 Pool Layer는 필터의 크기를 줄이면서 Max Pooling 기법을 사용한다. 이 경우, 눈이 있는 위치(값이 1인 부분)는 살리면서 전체 크기만 줄일 수 있게 되는 것이다.
이렇게 하면, 크기가 줄었으니, 파라미터 수가 감소하고, 그에 따라 overfitting될 확률도 낮아진다.
즉, 만약 위의 눈 filter예시에서 Pooling을 거치지 않고 FC로 들어간다면, 의미 없는 0의 값도 신경써서 학습하게 되므로 overfitting 될 확률도 높아지게 된다. Pooling은 이러한 불필요한 연산과 과적합을 막는 역할을 한다.
+) Max Pooling을 제외하고 Average pooling, L2-norm pooling 기법도 있는데, Max Pooling이 제일 많이 쓰인다고 한다.
- Softmax
마지막으로 알아볼 Layer는 Softmax Layer이다. AlexNet에서도 마지막에 존재하는 Layer인데, 이전에는 FC Layer가 존재한다. 따라서 Softmax의 입력값으로는 FC Layer의 Output인 1차원 벡터이다. 즉, 모델이 계산한 각 클래스별 score(점수) 값으로 이루어진 1차원 벡터가 입력으로 들어오는 것이다.
이때, 우리가 원하는 결과는 예를 들어, 차, 고양이, 비행기를 분류하는 모델이라고 할 때, 차 사진을 넣었으면 앞의 Layer를 거처 최종 결과로 [1,0,0]처럼 차일 확률이 1에 가깝게 나오기를 바란다. 그렇지만, FC Layer까지 거치면, 이 값이 score (점수)로 나타나게 된다. 예를 들어 차 사진을 넣었을 때는 [0.8, 0.2, 0.6] 처럼 score로 나오게 되는 것이다. 따라서 Softmax Layer에서는 이를 원하는 결과로 바꿔주는 역할을 한다.
그렇다면, 이를 어떻게 바꾸는 것일까?
앞서, FC LAyer의 출력은 각 클래스에 대한 score이다. 이 값들은 아직 "확률"이 아니다. 그렇기에 전체 합이 1이 되지 못한다. Softmax는 이 점수들을 확률 분포로 변환하는 함수이다.
이 함수를 수식으로 표현하면 다음과 같다.
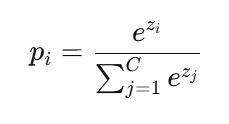
이때, 수식에 대해서 설명하면,
- pi = Softmax를 통과한 후 i번째 클래스일 확률
- C = 전체 클래스 개수
- zi = FC Layer에서 i번째 클래스에 대한 score
위 식을 보면, 모든 클래스의 출력을 지수함수로 변환한다는 것이다. 그런데 왜 지수함수로 변환시키는지 이유가 궁금했다.
Softmax를 거쳐 최종적으로 Loss를 계산하게 되고, 이 Loss는 다시 Backpropagation을 통해 미분되어야 한다. 따라서 출력 확률 pi는 연속적이고 미분 가능한 함수여야 한다.
그런데, 단순히 FC를 통해 얻은 score를 그대로 사용하면, 합이 1이 되지 않으며, 절댓값이나 max를 이용한 단순 정규화는 아래 그림과 같이 미분 불가능한 점이 존재한다. 이렇게 되면 NN의 기본 원리인 Gradient Descent를 적용할 수 없다.

그래서, Softmax에서는 지수함수를 사용하게 되는데, 지수함수를 적용하면 다음과 같은 특징이 있다.
- 모든 구간에서 미분 가능하며, 미분값도 단순하다. 따라서 Back Propagation이 안정적으로 진행 가능하다.
- 항상 양수이므로, 확률처럼 해석 가능하다.
- 큰 값의 차이를 더 극적으로 만들어준다. 가장 확실한 클래스에 더 높은 확률을 부여한다.
다음 예시를 한 번 살펴보자.
- FC Layer로부터 차, 개, 사람, 꽃, 비행기, 새에 대한 score를 [0.87, 3.2, 0.31, 7.2, 1.2, 0.4]로 받았다.
- 이를 Softmax를 적용하면 다음과 같이 결과가 나온다.
- [1.7e-3, 1.8e-2, 9.9e-4, 0.98, 2.4e-3, 1.1e-3]
즉, Softmax Layer는 높은 score를 더 높게, 낮은 score를 더 낮게 만들어 주는 효과가 있다. 그리고, 꽃이라는 score가 가장 높았고, Softmax를 거치면 확률이 0.98로 1에 가깝게 변했다.
이때 실제 우리가 원하는 모델의 출력은. 입력 이미지가 꽃이므로 [0, 0, 0, 1, 0, 0]과 같은 정답 확률 분포(One-Hot Vector)이다. 즉, 꽃 클래스일 확률이 1, 나머지는 0이 되는 것을 목표로 한다.
현재 모델의 예측 결과는 Softmax를 거친 확률 벡터 p = [p1, p2, p3, p4, p5, p6]이고, 정답 벡터 y와는 일치하지 않는다. 따라서 모델을 꽃 = 1일 확률에 가까워지도록 Loss를 최소화하고 나머지 클래스의 확률은 작아지도록 학습시켜야 한다.
- Cross Entropy
위 목표를 달성하기 위해 사용하는 대표적인 Loss Function은 Cross Entropy Loss이다.
위 예시에서 실제 출력을 y = [y1, y2, y3, y4, y5, y6]라고 하고 확률을 p = [p1, p2, p3, p4, p5, p6]라고 하면, 다음과 같은 식을 적용하는 것이다.

이 식을 적용하면, 정답 클래스일 확률이 1에 가까워질수록 L(Loss)는 작아지고, 확률이 0에 가까워지면 Loss가 엄청나게 커진다는 점을 알 수 있다.
예를 들어, 위 예시에서 Softmax를 거쳐 얻은 확률 중 가장 1에 가까운 값은 0.98로 꽃이었다. 이때, 발생할 Loss를 구하면, -log(0.98)로 그래프상 다음과 같이 위치한다는 것을 알 수 있다.

'학교공부 > [비디오이미지프로세싱]' 카테고리의 다른 글
| [비디오이미지프로세싱] - CNN_Activation Functions (0) | 2025.10.22 |
|---|---|
| [비디오이미지프로세싱] - Neural Networks (0) | 2025.10.18 |
| [비디오이미지프로세싱] - Linear Classification (0) | 2025.10.17 |
| [비디오이미지프로세싱] - 머신러닝(Linear Regression, Gradient Decsent) (0) | 2025.10.16 |



