지난 글에서는 블록체인에 적용된 기술들의 기본적인 핵심 원리에 대해서 정리해 보았다. 이번 글에서는 그중, Cryptography(암호화 기술)가 블록체인에 어떻게 사용되고 어떤 원리가 적용되었는지에 대해서 정리해 볼 예정이다.
1. Crypto란?
먼저, Crypto는 무엇일까? 영어의 접두어로, '암호_'라는 의미로 사용된다. Crypto가 붙은 대표적인 단어들은 다음과 같다.
- Cryptology(암호학): secret communication을 연구하는 학문
- Cryptography(암호화): secret 시스템 설계하는 기술
- Cryptanalysis(복호화): secret 시스템 해독하는 기술
즉, 암호학에은 크게 암호화(Cryptography)와 복호화(Cryptanalysis) 두 가지 분야로 나눌 수 있다.
또, 다른 단어들 중 Cryptography라는 것이 있는데, 정의하면 다음과 같다.
- Cryptograhpy(암호화 기술): cipher('비밀 코드'를 만드는)를 설계하는 학문으로, 수학적 원리를 기반으로 한 암호학의 한 분야이다.
2. Crypto의 목표
그럼 이 암호화 또는 암호학의 궁극적인 목표는 무엇일까? 다음과 같은 4가지 목표가 있다.
- Confidentiality(기밀성): 암호화의 최초 목적으로 정보가 허가되지 않은 사람에게 노출되지 않도록 보호하는 것
- Symmetric-key Ciphers(대칭키 암호)
- 하나의 키로 암호화와 복호화를 모두 수행
- 메세지와 암호키로 XOR 연산 수행(암호키와 암호문을 안다면 원문을 쉽게 유추할 수 있다는 단점 존재)
- Block ciphers: 블록 단위 (데이터 크기는 고정(128, 256, 512 ...)) 로 암호화, 각 블록은 동일한 키로 독립적으로 암호화.
- Stream ciphers: 데이터를 연속적인 비트 스트림 형태로 암호화
- Public-key ciphers: 공개키(Public Key)로 암호화하고, 개인키(Private key)로 복호화하는 방
- Symmetric-key Ciphers(대칭키 암호)
- Data Integrity(데이터 무결성): 데이터가 전송 중 변경, 손상, 위조되지 않았음을 보장
- 해시 함수
- 해시 함수를 이용해 고정된 길의의 해시값 생성
- 데이터 일부가 조금이라도 변하면 해시값이 달라지므로 위/변조 탐지 가능
- Message Authentication ceods(MACs): 키를 포함한 해시 함수로 생성되는 인증코드
- Digital signatures: 해시값에 서명도 검증하는 것. 해시값에 서명이 존재하지 않으면 해당 대상 무효.
- 해시 함수
- Authentitcation(인증): 데이터를 보낸 사람이 정당한 사용자임을 확인
- Entity authentication: 아이디 + 비밀번호로 인증하는 원초적인 방법
- Message authentication(= Data origin authentication): 메세지 출처 인증하는 방식, MACs + Digital Signatures로 인증
- Non-repudiation(부인봉쇄성): 송신자가 자신이 보낸 행위를 부인하지 못하도록 하는 것
- Digital signatures
- 일단 서명을 진행하면, 서명하지 않았다고 부인하지 못한다.
- 누군가가 개인키(Private key)를 도용해 대신 서명하더라도, 키를 보호하지 못한 책임은 자신에게 있음
- Digital signatures
따라서, 암호학의 기본 정의는 다음과 같다.
- cipher(암호화 알고리즘) 또는 cryptosystem은 plaintext(cleartext)를 암호화하기 위해 사용된다.
- 암호화의 결과는 ciphertext라고 한다.
- plaintext를 복구하기 위해 ciphertext를 decrypt(복호화)한다.
- 암호화 방식은 다음과 같은 3가지 종류가 있다.
- block ciphers: 블록단위 암호화
- stream ciphers: 연속적인 비트 스트림의 암호화
- hash functions: 해시함수를 이용한 암호화
- block ciphers와 stream ciphers는 암호화 key를 알면 복호화가 가능하지만, hash functions는 키 자체가 없기 때문에 단방향 암호화라고 할 수 있다.
- 또는 key 기반으로 분류할 수 있다.
- 0key: hash functions
- 1key: symmetirc ciphers - 복호화와 암호화를 하는데 동일한 key를 사용한다.
- 2keys: asymmetric ciphers - public key cryptosystem은 public key를 암호화하는데(또는 검증하는데), private key를 복호화(또는 서명하는데)하는데 사용한다.
암호학의 가정은 다음과 같다.
- 시스템(알고리즘)은 공격자를 포함한 모두에게 완전히 알려져 있다.
- key만이 보호되어 있다.(symmetric ciphers에서는 공격자는 key 자체를 모르고, asymmetric ciphers에서는 공격자는 public key는 알고, private key를 모르는 상태이다.)
- 즉, 암호화 알고리즘은 비밀인 상태가 아니다.
이런 가정을 하는 이유가 무엇일까?
- 알고리즘이 공개되어있는데도, 공격으로부터 계속 살아남았다는 것은 강하다는 증거이다.
- 언젠가는 취약점이 발견될 수 있긴 하지만, 비공개로 유지하다가 치명적인 순간에 뚫리는 것보다 공개 후 다양한 피드백을 통해 개선되는 것이 훨씬 낫기 때문이다.
+) 추가로 공인인증서의 해킹 사건에 대해서도 설명해주셨는데, 공인인증서는 public key와 private key를 기반으로 작동한다. public key는 이미 누구나 알고 있는 상태인데, 해킹 당시에 public key와 private key를 같은 위치(디렉토리)에 저장되어 있었다. 이로 인해 해킹 사건이 터졌을 때 문제가 생긴 것이다.
3. Cipher의 종류 - Random functions_Hash functions
이제 Cipher의 종류와 그 원리에 대해서 자세히 알아볼 예정이다.
먼저 알아볼 것은 해시 함수인데, 정의는 다음과 같다.
- Random functions_hash functions: input으로는 길이의 제한 없이 받아들이고, 고정된 길이(n bits라고 가정)로 output이 나오는 것.
해시 함수는 그래서, 압축 함수라고 불린다. Input의 길이와는 상관없이 항상 고정된 길이의 Output이 나오기 때문이다. 기본적인 해시 함수에 대해서는 자료구조 시간에 배웠기 때문에 이번에는 Cryptograhpic, 즉 암호학이 적용된 해시 함수에 대해서 중점적으로 정리해 보려고 한다.
- 암호학이 적용된 해시함수의 특징
- Collision resistance(충돌 저항성): 서로 다른 입력값에 대해 동일한 해시값이 출력되는 경우는 거의 발생하지 않는다.
- Preimage resistance(역상 저항성): 해시값이 주어졌을 때, 해당 해시값을 만든 입력값을 찾을 수 있는 것이 거의 불가능에 가깝다.
- 2nd preimage resistance(2차 역상 저항성): 입력값과 해시 함수 알고리즘과 출력값을 알 때, 해당 정보를 가지고 동일한 출력값을 가지는 다른 입력값을 찾기 힘들다.
그렇다고 해서, 다음과 같은 경우들이 존재하는 것도 아니다.
- 입력값: FOX > 해시함수 h() > 출력값: ABCD 2215 1111 2414 AK23
- 입력값: BOX > 해시합수 h() > 출력값: 254A DBD1 55DC 958S TK1D
즉, 글자가 하나만 다르다고 동일 해시함수를 적용했을 때 비슷한 출력값이 나오는 것도 아니다.
따라서 암호학이 적용된 해시 함수는 다음과 같은 기능을 제공하게 된다.
- Compression(압축): Input 크기와 상관없이 output 길이는 작아야 한다.
- Efficiency(효율성): Input이 주어졌을 때, Ouptut을 계산하기 쉬워야 한다.
- One-way(일방향성): 해시값이 주어졌을 때, 해당 해시값의 입력값을 찾는 것은 불가능하다. (=Pre-image resistance)
- Weak collision resistance: 입력값과 해시함수, 출력값이 주어졌을 때, 출력값과 같은 또 다른 입력값을 찾기 불가능하다. (= 2nd preimage resistance)
- Strong collision resistance: 서로 다른 x와 y에 대해서 해시값이 같은 경우가 발생하는 것이 불가능하다.
- Pre-Birthday Problem과 Birthday Pardox
위와 같은 특징들은 Pre-Birthday problem과 Brithday Paradox로 증명할 수 있다. Pre-Birthady 문제는 다음과 같다.
- N명의 사람이 방에 있다고 가정하자.
- 나와 생일이 같을 확률이 1/2 이상이 될 N은 무엇일까?
나의 생일과 다를 확률은 364/365이다. 그래서 전체 확률 1에서 (N명이 나와 모두 생일이 다를 확률)을 빼주는 것이 1/2 이상이면 된다. 식으로 나타내면 다음과 같다.
- 1/2 = 1-(364/365)^N
이를 계산하면, N = 253이다. 따라서 방 안에 253명 이상이 있어야 나와 생일이 같은 사람이 있을 확률이 1/2를 넘어서게 된다.
Birthday Paradox는 다음과 같다.
- 방 안에 N명이 사람이 있다고 가정하자.
- 이때, 랜덤으로 N명 중 2명을 뽑아 생일이 같을 확률이 1/2을 넘어설 때는 언제일까?
답은 N = 23 이다. 즉, 23명 이상이 있어야 N명 중 2명을 뽑아 생일이 같을 확률이 1/2을 넘어서게 된다. 이를 구하는 방법은, 확률과 통계에서 배운 "365개의 공을 상자에 무작위로 넣을 때, 같은 상자에 공이 두 개 이상 들어가는 확률" 문제와 동일하다. 즉, 다음과 같은 풀이 과정을 거친다.
- 첫 번째 사람의 생일이 적힌 공을 바구니에 넣는다.
- 두 번째 사람의 생일이 적힌 공을 바구니에 넣는다.
- 이때 첫번째 사람이 넣은 바구니에 넣을 순 없다. 따라서 생일이 겹치지 않을 확률은 1 - 1/365이다.
- 세 번째 사람의 생일이 적힌 공도 바구니에 넣는다.
- 이때 동일하게 첫번째, 두번째 바구니에는 넣을 순 없다. 따라서 겹치지 않을 확률은 1 - 2/365이다.
이를 일반화 시키면, 다음과 같은 식이 나온다.
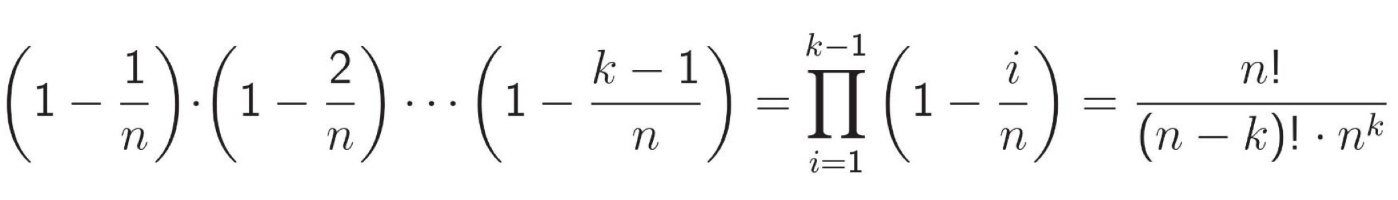
따라서 이 식의 값이 1/2보다 크게 하는 k를 찾으면 k = 23이다. 이는 대략 √365 이다. 즉, √n 규모에서 충돌 확률이 급격하게 상승하게 된다.
결국, Pre-Birthady problem과 Birthday Paradox에 대해서 정리하면 다음과 같다.
- Pre-Birthday problem: 한 방에 한 명의 생일을 기준으로 해당 사람과 생일이 같은 사람이 존재할 확률이 1/2 이상이 되기 위한 N = 253,
- Birthday paradox: 한 방에 무작위 두 명을 골랐을 때 생일이 같을 확률이 1/2 이상이 되기 위한 N = 23이다
두 문제는 "타깃(특정 값)에 대한 일치 찾기"와 "임의 쌍의 일치 찾기"라는 관점에서 다르기 때문에 N에 큰 차이가 생긴다.
이제 이 차이를 해시 함수에 적용하면 직관적으로 이해하기 쉽다.
- 해시 함수 출력값이 n비트이면 가능한 해시 값의 개수는 2^n개 이다.
- 타깃 해시값(특정 해시값에 대응하는 입력을 찾는 문제, preimage)을 찾으려면 평균적으로 2^n번의 시도가 필요하다.(=Pre-Birthday problem)
- 아무 두 입력이 충돌하는 쌍을 찾는 것은 약 2^n/2 번 시도만으로 충돌이 발생할 확률이 1/2이다. (=Birthday Paradox)
따라서 해시 길이 n비트의 충돌 저항성은 실질적으로 n/2비트의 보안 수준을 제공한다고 볼 수 있다.
예를 들어 비트코인을 생각해보자. 비트코인은 앞서 SHA-256(해시 출력값: 256bit)라는 해시 함수를 사용한다고 정리했다.
- 충돌을 찾기 위한 계산량은 2^(256/2) = 2^128번이다.( = Birthday Paradox)
- 프리이미지(preimage) 공격은 2^256번 시도해야 한다.(=Pre-Birthday Problem)
이 값들은 현재, 충분히 커서 공격으로부터 아직까지는 안전하다고 평가된다. 그렇지만 이론상 언젠가는 깨질 수 있다, 그렇지만, 이럴 때는 해시 길이를 늘려 SHA-512를 사용하는 등 다양한 방법이 존재한다.
- 유명한 Cryptographic 해시 함수들
- MD5 : Rivest라는 MIT가 발명했고, 현재는 더 이상 쓰이지 않는 해시 함수.
- 128bit의 해시값(output)을 가지고, 충돌을 찾기(=해시를 깬다)는 쉽다. (Why? - 2^64만 시도하면 되기 때문에)
- SHA - 1 : NSA(국가안보국)이 설계하고, NIST가 표준으로 채택한 Secure Hash Algorithm의 첫 번째 버전
- 160 bit의 해시값(output)을 가진다.
- 2017년 구글이 공격 성공 사례를 발표하면서 더 이상 안전하지 않다고 판단, 사용하지 않는 해시 함수로 됐다.
- SHA - 2 family
- SHA-1를 개선한 비슷한 구조를 가진 알고리즘이다.
- SHA-224, SHA-256(블록체인에서 선택한 알고리즘), SHA-384, SHA-512
- 아직까진 안전한 해시 함수로 평가된다.
- SHA - 3 family: Keccak(원래 알고리즘 이름)이 NIST 공모전에서 우승하면서 SHA-3으로 표준화되었다.
- SHA-1/2와 다른 수학적 알고리즘을 지닌다.
- SHA3-224, SHA3-256, SHA3-384, SHA3-512
- Cryptographic Hash 함수의 적용
그럼 실제로 어떻게 적용되고 활용되며, 인증은 어떻게 진행되는지 알아보자. 쉬운 예시로 사용자의 아이디 비밀번호를 예시로 들어보자.
- 회원가입을 진행하고, 아이디와 비밀번호를 저장한다.
- 사용자가 비밀번호를 입력하면, 서버는 해시 함수를 적용한 결과값을 DB에 저장한다.
- 원래 비밀번호가 123456789라면 해시 적용 결과가 hadegtq152 같은 값으로 저장될 수 있다.
- 해시 함수는 단방향 함수로, 해시값으로부터 원래 비밀번호를 복원하는 것은 계산적으로 어렵다.
- 사용자가 로그인 화면에 비밀번호를 입력하면, 서버는 같은 해시 함수를 적용해 나온 결과를 데이터베이스에 저장된 해시값과 비교한다.
- 또는 인증기관에서 해시 함수를 적용해서 해시값과 같은지 비교해서 인증만 해준다. 따라서 디비가 유출되어도 비밀번호는 해시값으로 저장되어 있기 때문에 안전하다.
- 공격 난이도
- 해시 결과값이 10bit라고 위와 같이 생각하면 123456789에 대해서 총 2^10을 시도해야 해시를 깰 수 있다.
- 또한, 123456789가 아닌 해당 해시값과 동일한 해시값을 가지는 input을 찾는 것은 2^5번 시도해야 한다.
4. Cipher의 종류 - Random generators_Stream ciphers
다음으로 Random generators인 Stream ciphers에 대해서 알아보자. 이를 정의하면 다음과 같다.
- Random gerators: 짧은 Input으로 긴 Output을 생성한다.
- Stream ciphers: Random generator(키 스트림 생성기)가 만들어낸 키 스트림을 plaintext와 XOR 연산하여 ciphertext를 생성하는 암호화 알고리즘이다.
이때, random generator로 키 스트림을 생성하고 이를 통해 암호화를 진행하는데, 그럼 어떤 방식의 random generator를 사용할까?
- Random Bit Generation
보통 key와 nonce를 생성하기 위해서는 예측 불가능한 비트가 필요하다. 이러한 난수를 만드는 방법은 다양한데, 차례대로 살펴보자
- Seed 기반 난수 생성: 컴퓨터 환경에서 자주 사용하는 방식으로 보안된 seed(시드) 값을 바탕으로 난수를 생성하는 것이다. Pseudo-Random Number Generator(PRNG)가 seed를 입력받아 일련의 난수를 만들어낸다.
- 이때, 한계점이 존재하는데, PRNG는 '난수처럼 보이는' 수를 생성한다. 즉, 난수를 생성하긴 하지만, 어느 순간 규칙이 존재하게 된다. 따라서 보안적으로 완전한 난수를 만들 수는 없다.
그래서, 완전한 난수를 만들어내는 방법들이 존재하는데, 다음과 같다.
- H/W 기반으로 random bit generate: 하드웨어에 있는 Random bit generator 사용 (thermal noise(열 잡음) 등)
- 사용자 행동 기반 random bit generate: 키보드 입력 간격, 마우스 움직임, 터치 패턴 등을 소스로 활용
- H/W 응답 시간 기반 random bit generate: 디스크 드라이브의 회전 속도, I/O 응답 시간 지연 등 시간차 소스로 활용
- 디지털/아날로그 변환기 노이즈: 사운드 카드나 카메라 센서의 전자적 노이즈를 소스로 활용
- 네트워크 기반: 패킷 전송 시간, 도착 순서 등을 소스로 활용
- 시스템 정보 기반: PID(Process ID), CPU 클럭 타이밍, 메모리 접근 시점 등의 상태를 소스로 활용
그러나, seed 기반 난수 생성을 포함해 위의 방법들은 완벽하지 않다. 이를 또 해시 함수를 적용하면 통계적으로 더 좋은 난수를 생성할 수 있다.
그럼에도, Stream cipher은 PNRG 기반으로 키 스트림을 생성하고, 그 키 스트림을 평문과 XOR하여 암호문을 만든다. 생성된 키 스트림은 평문과 같은 길이여야 한다. 그렇지만, 동일한 키로 다른 Input과 XOR 연산을 한다면, 치명적인 보안 약점이 드러난다. 따라서, 이를 방지하기 위해 현대 Stream cipher는 seed + nonce 조합을 활용한다.

즉, 그림에 대해서 설명하면,
- seed(비밀키)를 PNRG에 입력하여 키 스트림을 생성한다.
- 생성된 키 스트림과 plain text를 XOR 연산을 진행한다.
- 연산 결과가 ciphertext가 된다.
- 복호화는 동일한 키 스트림을 생성해 ciphertext와 XOR 연산을 진행하면 된다.
이때, 키스트림 재사용을 방지해야 한다. 키 스트림 재사용은 같은 seed로 plaintext를 2번 XOR 연산을 진행하여 각각 ciphertext를 만든다는 것인데 이때 다음 그림과 같이 식이 정리된다.
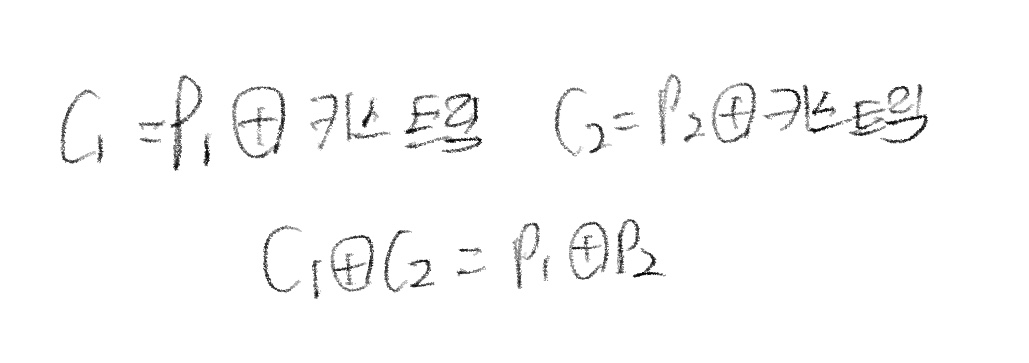
이때, plaintext간 관계를 ciphertext를 통해 유추할 수 있고, 하나의 plaintext라도 알게 되면 나머지도 모두 알게 되므로 주의해야 한다.
5. Cipher의 종류 - Random permutations(무작위 순열)_Block ciphers
다음으로 알아볼 cipher는 Block cipher이다. Block cipher는 다음과 같다.
- Block ciphers: 1개의 key를 이용해 고정된 사이즈의 input을 고정된 사이즈의 output으로 바꾸는 암호화 기법
이때, Block ciphers는 Random permutations(무작위 순열) 방식을 이용하는데, Random permutation에 대해서 알아보자.
- Random Permutations
2 bit를 예시로 설명해 보자. 2bit 크기의 블록이 존재한다면 블록의 총 종류는 (00), (01), (10), (11)로 4가지이다. 이때, 각각의 블록을 본인 제외 다른 블록들과 1대1로 대응시키는 하나의 순열을 선택한다.
- 00 - 01
- 01 - 10
- 10 - 11
- 11 - 00
즉, 왼쪽은 plaintext 블록, 오른쪽은 ciphertext 블록이다. 이 순열을 어떤 방식으로 선택하는지가 key에 의해 결정된다.
따라서 block cipher는 plaintext 블록에 대해, key가 선택한 특정 순열을 적용해 ciphertext 블록을 만드는 방식이다. 이러한 방식의 블록 암호가 안전하려면 confusion과 diffusion이 중요하다. 각각은 다음을 의미한다.
- confusion: key와 ciphertext 사이의 관계를 최대한 복잡하게 만들기
- diffusion: plaintext의 한 비트가 바뀌면 ciphertext의 많은 비트들이 변하도록 만드는 성질
위 두 특징은 통계적 관계를 분석해서 키 정보를 추론할 수 없게 막기 위해 중요한 특징이다.
- 관련 알고리즘
과거에는 DES알고리즘이 널리 사용되었지만, 키 길이가 너무 짧아서 현대 공격에서 안전하지 않기 때문에 더 이상 사용되지 않는다.
이를 대체하기 위해 1990년 후반에 AES 공모가 진행되었고 이 과정은 미국 NIST(National Institue of Standard and Technology)가 주관했다.
AES는 Rijndael이라는 알고리즘이 최종 선정된 것으로, 128bit 블록 크기를 기반으로 128, 192, 256 bit 키 사이즈의 여러 버전을 제공한다.
6. Cipher 종류 - Public key encryption(special kind of block cipher)
public key 암호화는 block cipher의 특별 케이스 중 하나로, 서로 다른 두 개의 key(public key, private key)를 사용하기 때문에 asymmetric cipher라고도 불린다. 이 방식의 아디이어는 다음과 같다.
- 누구나 암호화할 수 있지만, 복호화는 key의 소유자만 가능하다.
이 방식은 크게 두 가지로 나뉠 수 있는데 다음과 같다.
- Public key로 암호화, Private key로 복호화
- 공개키 암호화는 계산 비용이 매우 크기 때문에 대용량 데이터 암호화와 같은 block cipher 대체용으로는 사용하지 않는다.
- Private key로 만든 Digital Signature(전사 서명) 후 public key로 검증
- 비트코인 블록체인에서 사용하는 방식으로, 비트코인 UTXO 소유자가 서명한 트랜잭션이 정말 그 소유자에 의해 만들어졌는지 검증할 때 사용된다.
이런 비대칭 암호화 방식에는 RSA, Diffie-Hellman, Elliptic curve 방식이 있는데, 차례대로 정리해 보려고 한다.
- RSA
이 방식은 엄청 큰 두 소수(prime #)를 곱했을 때 나온 수 n이 주어졌을 때, 이 n을 보고 두 소수를 유추하기 어렵다는 수학적 성질을 이용한 방식이다. 이 방식은 많이 사용되었지만, 더 긴 키 길이를 필요로 하고, ECC 같은 더 효율적인 알고리즘이 등장하면서 사용 비중이 줄어들고 있다.
이 방식에 대해서 정리하면 다음과 같다.
- p와 q를 큰 소수라고 하고, N = pq라고 하자.
- 이 N은 modulus 연산에 사용된다.
- e를 (p-1)(q-1)의 서로소로 선택한다.
- ed = 1 mod (p-1)(q-1)을 만족하는 d를 찾는다.
- 이때 Public Key는 (N, e), Private Key는 d이다.
- 이때, Message M을 보낸다고 했을 때, M < N 이어야 한다.
- M을 암호화하기 위해서는 C = M^e mod N을 계산해야 하고, 이 C가 바로 Ciphertext이다.
- C를 복호화하기 위해서는 M = C^d mod N을 계산해야 한다.
- e와 N은 공개되어 있지만, 누군가 N을 p와 q로 인수분해할 수 있다면, e를 알 수 있고, 결국 d를 쉽게 구할 수 있기 때문에 RSA가 깨진다.
따라서 이 방식은 p, q를 유추할 수 있으면 안되는 아주 큰 소수로 정해야 한다.
- Diffie-Hellman
이 방식은 두 사용자가 안전하게 공유된 대칭키를 생성하기 위해 사용하는 key exchange 방식이다. 즉, 실제 메시지를 Diffe-Hellman 방식으로 암호화/복호화하는 것이 아닌, 이 과정을 통해 두 사람이 동일한 대칭키(symmetric key)를 얻고, 이후 그 대칭키로 암호화를 수행한다.
방식은 다음과 같다.
- p와 g는 공개되어 있다.
- A의 private key를 x, B의 private key를 y라고 하자.
- A는 g^x mod p를 계산하여 B에게 보낸다.
- B 는 g^y mod p를 계산하여 A에게 보낸다.
- A는 B로부터 받은 값(g^y mod p)을 이용해, (g^y)^x mod p = g^(xy) mod p를 계산한다.
- B도 A로부터 받은 값(g^x mod p)을 이용해 (g^x)^y mod p = g^(xy) mod p를 계산한다.
- 이를 통해 두 사람은 서로 다른 정보를 주고 받았지만, 결과적으로 동일한 대칭키 K = g^(xy) mod p를 얻게 된다.
이 방식은 중간 공격자가 A와 B 사이에 오가는 값을 보더라도, x나 y를 모르기 때문에 g^(xy) mod p, 대칭키를 알 수 없다. 이 Diffie-Hellman 방식으로는 서명을 하거나 암호화/복호화를 진행할 수 없다.
- Elliptic Curve Cryptograhpy(=ECC)
Elliptic curves는 공개키 암호를 구현하는 완전히 다른 수학적 접근 방식이다. 특히 블록체인에서는 ECDSA(Elliptic Curve Digital Signature Algorithm) 형태를 사용한다.
ECC를 사용하는 이유는 RSA와 비교하여 다음과 같다.
- 같은 보안 수준을 훨씬 짧은 키 크기로 달성 가능하다.
- RSA 2048 bit 는 대략 ECC 256 bit 보안 수준과 비슷하다.
- 키가 짧아짐에 따라 저장 공간이 적게 들며 계산량도 훨씬 줄어들게 된다.
- 더 빠른 연산이 가능하다.
- ECC는 RSA에 비해 서명, 검증, 키 생성 등이 빨라 비트코인처럼 수많은 서명을 처리하는 시스템에 매우 적합하다.
- 저장 공간과 bandwidth 절약한다.
- 공개키와 서명의 크기가 작아 블록체인의 블록 크기 감소에도 기여한다.
그렇지만, RSA는 오랜 시간동안 여러 공격을 견뎌 온 검증된 방식이기 때문에 기존 시스템과의 호환성 등의 이유로 아직 널리 사용되고 있다.
그럼, Elliptic Curve, 타원 곡선은 무엇일까? 타원 곡선 기본 형태는 다음과 같다..

이 방식에 modular 연산을 적용하면, 암호학에서 사용하는 유한체 위의 타원 곡선이 된다.

이때 p는 큰 소수이며, 타원 곡선 위의 점들은 정수 좌표(0 <= x, y <= p-1)와 특수한 점인 point at infinity만 존재한다.
암호학을 적용한 타원 곡선 식이 아닌, 기본 타원 곡선은 다음과 같이 표현된다.
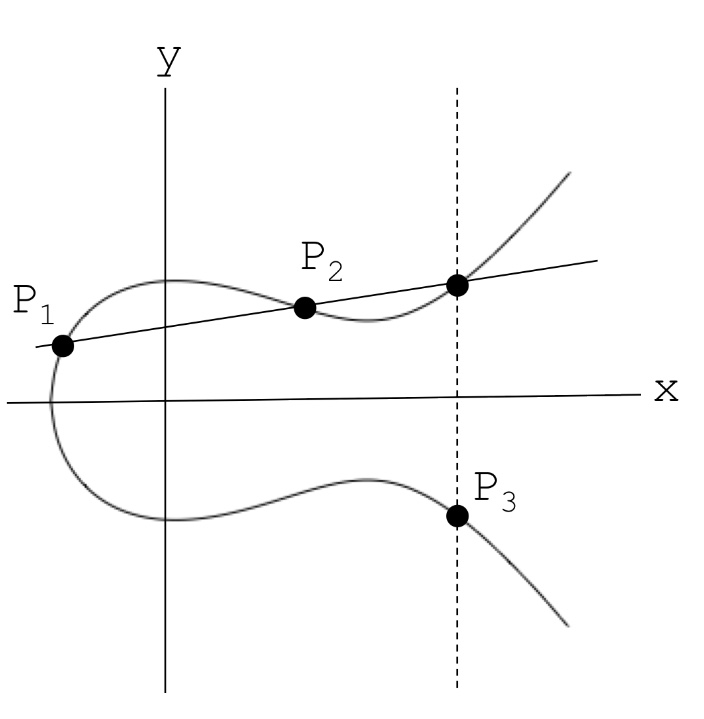
해당 그래프를 E: y^2 = x^3 - x + 1에 대한 그래프라고 하면, 독특한 점 연산을 정의할 수 있다. 예를 들어 위 그림과 같이 P1, P2가 있을 때, 다음과 같이 정의한다.
- P3 = P1 + P2
타원 곡선에서의 덧셈은 일반적인 덧셈이 아니라 다음 규칙을 따른다.
- P1과 P2를 지나는 직선을 그린다
- 해당 직선이 타원 곡선과 다시 만나는 점을 P4라고 하자.
- 이때 P4를 x축 대칭이동하면, 그 점이 P3가 된다.
즉, 직선이 곡선과 마지막으로 교차하는 점을 찾고 그 점을 y축에 대칭 이동한 점이 P3가 되는 것이다.
다른 예시를 한 번 들어보자.
- y^2 = x^3 + 2x + 3 (mod 5)
- 이렇게 되면, x와 y는 0~4(p-1)의 정수 점과 point at infinity로 제한된다.
이때, x = 0 ~ x = 4까지 대입해서 y 값을 구해보면 다음과 같다.
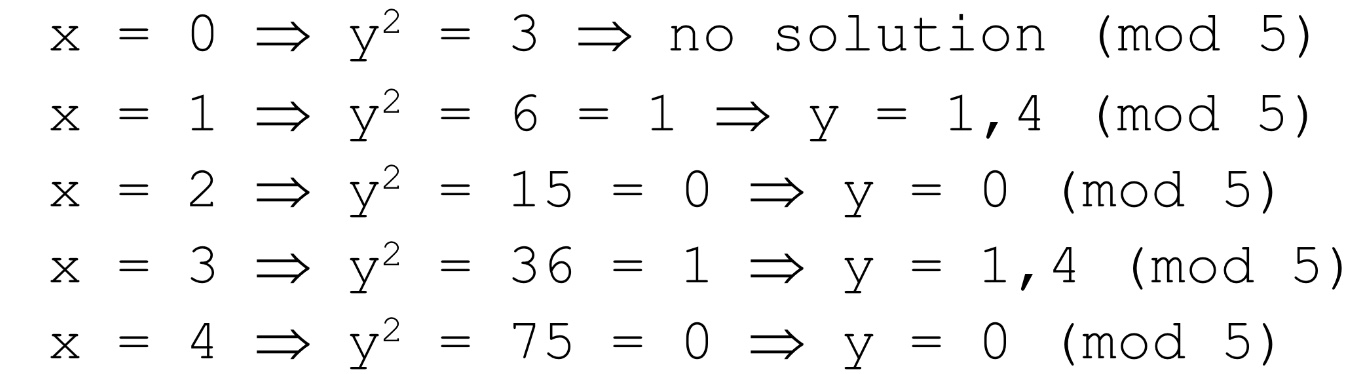
따라서, 타원 곡선 상의 점은 다과 같다.
- (1, 1), (1, 4), (2, 0), (3, 1), (3, 4), (4, 0)과 point at infinity
그럼 이때, (1, 4) + (3,1) = P3라 할 때, P3는 어떻게 구할까? 모듈러 연산이 존재할 때의 타원 곡선 상의 + 연산은 다음과 같이 왼쪽 그림과 같이정의되며, 이를 활용한 연산은 오른쪽 그림이다.


따라서, 이 타원 그래프에서는 P3 = (2, 0)으로 정의된다.
- ECC Diffie-Hellman
그럼 ECC와 Diffie-Hellman 방식을 결합한 방식을 한 번 살펴보자. 다음과 같은 타원 곡선이 존재하고, Alice와 Bob의 private이 있다고 가정하자.
- y^2 = x^ 3 + 7x + 3 (mod 37)과 곡선 상의 점 (2, 5)
- Alice's private key = dA = 4
- Bob's private key = dB = 7
이때, Alice는 Bob에게 4 (2,5) = (7, 32)를 보낸다. 이때, 4 (2, 5)는 또 새로운 연산으로 (2, 5) + (2, 5) + (2, 5) + (2, 5)를 진행한 값이다. Bob은 Alice에게 7 (2,5) = (18, 35)를 보낸다.
Alice와 Bob은 각각 다음을 계산한다.
- Alice: 4 (18, 35) = (22, 1)
- Bob: 7 (7, 32) = (22, 1)
이를 통해 Alice와 Bob은 대칭키를 얻고, 보내려는 메시지에 해당 대칭키를 적용해 둘 만 복호화할 수 있는 안전한 통신이 가능해진다.
- ECC Signature and Verification
이제는 ECC를 통한 서명과 검증 방식에 대해서 정리해 보려고 한다. 방법은 다음과 같다. 아래 과정은 블록체인에서 사용되는 ECDSA의 기본 구조이다.
- 서명 과정
- z = hash(m)을 계산한다. 이때, m은 서명하려는 실제 메시지이다.
- 무작위 숫자 k를 선택한다. 매 서명마다 반드시 새로운 k를 사용해야 하며, 재사용 시 보안이 깨진다.
- 타원 곡선 상의 점 (x1, y1) = kG를 계산한다. 이때, G는 타원 곡선의 base point(모든 연산의 출발점)이다.
- r = x1 mod n을 계산한다. 이때, n은 G의 order(nG = point at infinity를 만족하는 n)이다.
- s = k^(-1) (z + rdA) mod n을 계산한다. 이때, dA는 Alice의 Private key다.
- 서명 (r, s)가 만들어진다.
- 검증
- z = hash(m)을 계산한다.
- u1 = zs^(-1) 과 u2 = rs^(-1) mod n을 계산한다.
- 곡선 상의 점 (x1, y1) = u1G + u2QA를 계산한다. 이때 QA = dA G이며, QA는 Alice의 Public Key이다.
- 계산된 x1과 r을 비교했을 때, r = x1 mod n이라면 서명이 유효한 것이며, 다른 경우 유효하지 않다고 판단한다.
7. Public-key infrastructure(PKI)
PKI는 공개키가 실제로 누구의 것인지 보증해주는 시스템이다.
공개키 암호화는
- private key로 해독을 하거나
- pirvate key로 만든 서명으로 public key를 검증
할 수 있다. 그렇지만, 그 공개키가 특정 누구의 것인지 확인할 방법이 없다. 예를 들어 어떤 사람 B가 Alice인 척을 본인(B)의 public key를 제시하면서 이걸로 암호화해서 자신에게 보내도록 유도하면, 상대방은 이를 Alice의 공개키라고 오해하고 B에게 데이터를 보내게 된다. 이때 B가 악의적인 사람이라면 중요한 정보를 그대로 탈취당하게 된다. 이를 방지하기 위해 신뢰할 수 있는 제 3자(CA)가 등장한다.
CA는 Alice에 대한 인증서를 다음과 같이 만들어서 서명한다.

이 Certc(A)에 대해서 설명하면 다음과 같다.
- A: Alice
- KA: Alice의 공개키
- T: 이 인증서의 시작 시각
- L: 유효시간
- Kc: CA의 개인키로 서명한 값
정리하면, 이 공개키 KA는 Alice의 것이며, 시간 T부터 L 동안 유효하다는 것을 CA가 서명해서 보장해주는 것이다.
CA의 서명이 필요한 이유는 다음과 같다.
- 누구나 내가 Alice다라고 말하면서 엉뚱한 public key를 제안할 수 있다.
- 하지만 CA의 개인키로 서명된 인증서는 오직 CA의 공개키 Kc로만 검증된다.
- 브라우저나 OS는 이미 신뢰할 수 있는 CA들의 공개키 목록을 가지고 있다.
즉, Alice가 아닌 사람이 본인이 Alice인 것처럼 주장하여 임의의 public key와 CA를 제안한다고 해도, 브라우저나 OS는 미리 저장된 신뢰할 수 있는 CA 공개키 목록을 이용해 해당 인증서가 실제 CA의 서명인지 검증할 수 있다. 따라서 CA 서명 검증이 성공하는 순간, 인증서에 포함된 공개키의 소유자 신원이 보장된다.
Alice의 public key를 Certc(A)로부터 추출하기 위해 다음과 같은 연산을 정의한다.
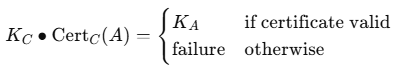
이 연산은 다음과 같은 특징을 지닌다.
- CA의 공개키 Kc로 인증서에 붙어 있는 CA 서명을 검증한다.
- CA 위조 여부 확인
- 인증서 내부의 다른 조건도 체크한다.
- 유효 기간
- 인증서 포맷
- CRL/OCSP 등에서 폐기 여부
- 예를 들어, Alice의 개인키가 있던 스마트 카드가 도난되거나 저장하고 있던 서버가 털리게 되면, 공개키 자체는 그대로이지만 private key가 노출된 것이므로 그 공개키는 더 이상 안전한 신원확인 수단이 아니다.
- 따라서 CA는 즉시 CRL(Ceritifcate Revocation List)에 넣어 폐기 상태로 만든다.
- 모든 조건이 만족되면 인증서 내부에 있던 Alice의 공개키 KA를 신뢰할 수 있는 공개키라고 반환한다.
8. Hybrid Encryption(디지털 봉투)
이제 공개키 암호와 대칭키 암호를 섞어서 쓰는 예시를 한 번 살펴보려고 한다. 다음 그림을 참고하자.

그림에 대해서 설명하면 다음과 같다.
- Alice는 plaintext를 임의의 Secret key로 AES 방법을 통해 Ciphertext를 생성한다.
- 그 다음, 이 Secret Key를 Bob의 공개키로 RSA 암호화한다.
- Alice는 Bob에게 Ciphertext와 암호화된 Secret Key 2개를 보낸다.
- Bob은 두 데이터를 받고, 자신의 private key로 암호화된 Secret key를 복호화하여 원래 Secret Key를 얻는다.
- Secret Key를 얻은 Bob은 그 secret key로 Ciphertext를 복호화하여 plaintext를 복원한다.
즉, 정리하면 메시지는 빠른 대칭키(AES 등)로 암호화하고, 그 대칭키 자체는 RSA로 안전하게 암호화하여 전달하는 방식이 바로 Hybritd Encryption이다.
9. 전사서명 동작원리
전자서명은 다음과 같이 동작한다.
- Sender는 보내려는 메시지 M을 해시한 값 hash(M)에 본인의 private key로 서명을 한다.
- 그 후, Sender는 보내려는 메시지 M(plaintext)와 Sign(private key, hash(M)) 총 두 개를 보낸다.
- Reciever는 Sender의 public key를 통해 Sign(private key, hash(M))을 복호화한다.
- 복호화한 후, hash(M)을 얻고, 받은 메시지 M'(plaintext)에 대해 hash값을 적용한다.
- 이때, hash(M') = hash(M)이라면 sender의 서명이 유효하다고 판단한다.
'학교공부 > [블록체인]' 카테고리의 다른 글
| [블록체인] - 비트코인_트랜잭션 (0) | 2025.12.11 |
|---|---|
| [블록체인] - 비트코인 (0) | 2025.12.11 |
| [블록체인] - 비트코인의 기술적 특징 (0) | 2025.10.12 |
| [블록체인] - 비트코인과 현금 (0) | 2025.09.29 |
| [블록체인] - 비트코인 프롤로그 (0) | 2025.09.29 |
